- Arithmétique : divisibilité, PGCD et PPCM, Nombres premiers
- Des mathématiciens célèbres : Fermat et Gauss
- Fonction exponentielle - Fiche de Cours terminale
- Le raisonnement par récurrence : principe et exemples rédigés
- Limites de fonctions - Cours sur les limites
- Fiche sur les nombres complexes - terminale
- Cours sur les suites en Terminale S
Inscription / Connexion Nouveau Sujet
Propagation d'une note- Le PageRank
Bonjour, j'ai un dm à faire et je n'arrive pas à résoudre le problème suivant :
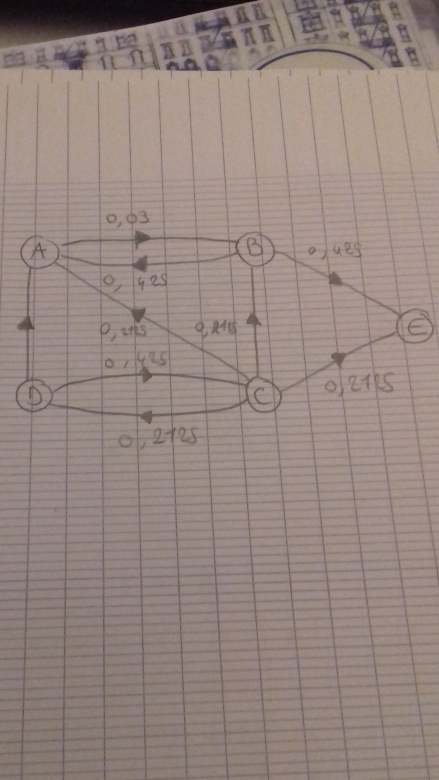
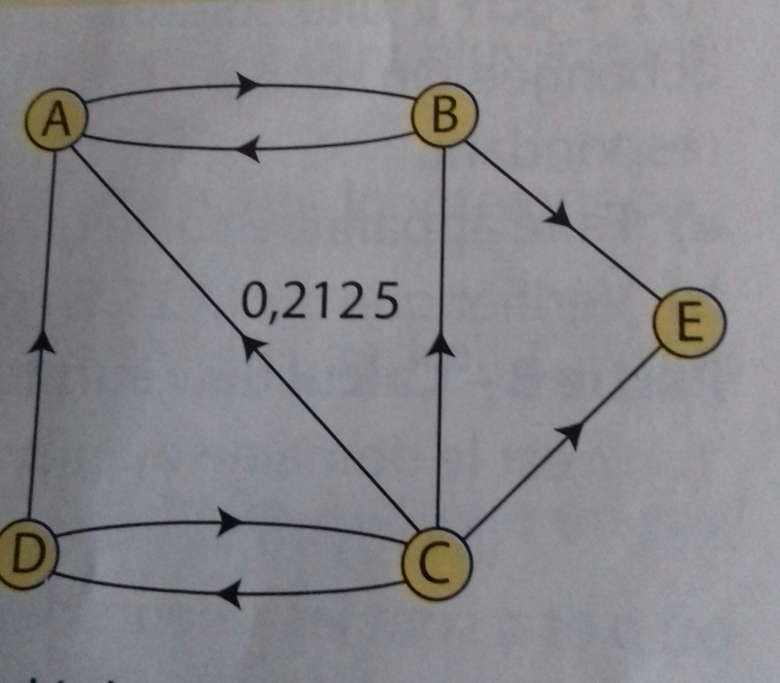
On suppose que le Web est composé de 5 pages A,B,C, D et E où les liens d'une page à l'autre sont représentés par le graphe ci-contre :
Le PageRank peut-être calculé de manière itérative.
Initialement chaque page a la même note k où :
k= 0.15 (nombres de pages)
(0.15 est appelé le coefficient d'échappement).
D'une étape à la suivante, chaque page reçoit une nouvelle note héritée des pages qui lui donnent accès :
- chaque page donne 85% de sa note précédente aux pages dont elle donne accés et ce de manière équitable entre celle-ci ;
- chaque page reçoit en supplément la note k.
a) La page C donne accès à quatre pages A,B, D, E ; elle partage donc de manière équitable 85% de sa note entre ces quatre pages. Ainsi, on note 0.2125 sur le lien C A du graphe.
A du graphe.
Compléter le graphe par les parts des notes reversées.
b) On note respectivement an, bn, cn, dn, et en les notes des pages A, B, C, D, et E à l'étape n.
Montrer que pour tout nombre entier n :
an+1= 0.03 + 0.425bn + 0.02125cn + 0.425dn
c) Déterminer de même les relations de récurrence concernant les autres suites.
Merci pour vos réponses 
Mais je ne comprends toujours pas pourquoi 0.03 dans le résultat du b) et non 0.85 ?
Je dois bien utiliser la formule P=PxM ?
le 0.03 provient de 0.15/5
dans les relations de récurrence , tu dois ajouter les entrées et non les sorties