Inscription / Connexion Nouveau Sujet
Pyramide
Bonsoir
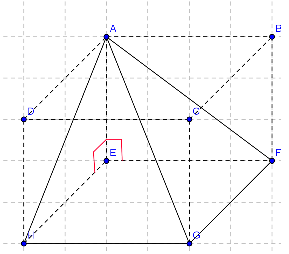
J'ai un exo à faire, mais dans la figure ci-dessous, je dois trouver le volume de la pyramide, mais c'est quoi la hauteur dans tout ça ?
Merci
Louisa 
Bonsoir,
La hauteur de cette pyramide est AE car la droite (AE) relie le sommet à la base de la pyramide et cette droite est perpendiculaire à la base EFGH.
Ah ok ! et bonsoir à vous 2, merci j'ai même pas pensé à [AE]
et pour écrire quelle fraction du parallépipède qu'occupe la pyramide, est'ce qu'il y a une formule ou autre...?
Merci
On pose : a=EH ; b=EF ; c=AE
Volume du parallélépipède : a*b*c
Volume de la pyamide : (1/3)a*b*c (car V=(1/3)*airebase*hauteur)
La fraction du paralélépipède occupé par la pyramide est donc de 1/3.
Je poste mon exercice, c'est beaucoup plus facile maintenant que je connais la hauteur :
Dans le parallépipède ABCDEFGH, AB = 8 cm ; AD = 6 cm ; AE = 5 cm.
a. Quel est le volume de la pyramide ?
J'ai calculé l'aire de la base EFGH = 8 * 6 = 48 cm²
AE est donc la hauteur de la pyramide, donc (48 * 5)/3 = 80 cm3.
b. Quelle fraction du volume du parallépipède occupe la pyramide ?
Volume du parallépipède = 8 * 6 * 5 = 240 cm3
Mais pour la fraction je fais 80/240 ?
Merci
Les résultats me paraissent justes. Pour la fraction, il faut effectivement faire 80/240 ce qui fait après simplification 1/3 (on retrouve donc le même résultat que celui que je t'avais indiqué plus haut, valable quelles que soient les longueurs des côtés).
Bonjour à tous,
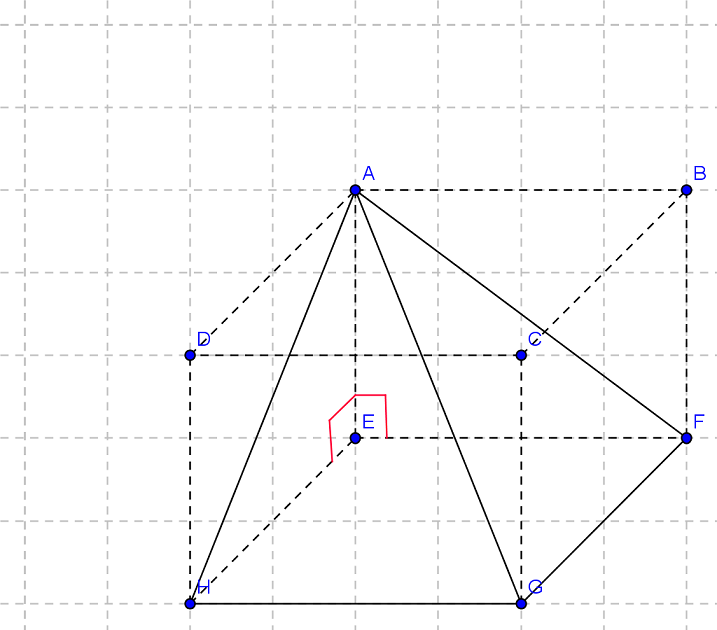
Louisa >> Voici un exemple de redimensionnement de l'image avec Picture Manager (livré avec Windows) :
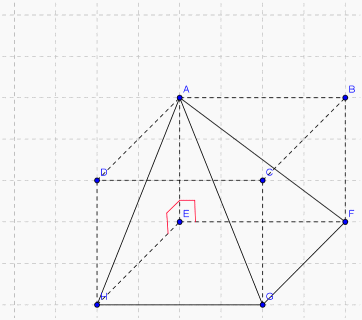
Les dimensions de la première image ont été multipliées par 50 % (donc divisées par 2  )
)

Ca y est Coll, j'ai bidouillé l'image, je l'ai retourné dans tous les sens pour enlever le plus possible de quadrillage, et voilà !