Inscription / Connexion Nouveau Sujet
Pyramide, droite et plan
Bonjour ,
dans le but de m'exercer pour le Bac je réalise actuellement un exercice qui me pose quelques difficultés ...
En voici l'énoncé :
SABCD est une pyramide à base carrée telle que les triangles ABS et ADS sont isocèles rectangles en A.
I,J et K sont les milieux respectifs des segments [AB], [AD] et [SC].
1- Le but de cette partie est de déterminer les positions des points N et P respectivement sur [SB] et [SD]. On se place dans le repère orthonormé (A;AB;AD;AS)
a- Déterminer les coordonnées des points I,J et K
b- En déduire une équation du plan (IJK)
c- Donner une représentation paramétrique de la droite (SB)
d- En déduire les coordonnées du point N et vérifier que BN=1/4BS
e- Déterminer de même la position du point P sur le segment [SD]
Je bloque à partir de la question 4 car ma vérification est fausse donc mon exercice doit comporter une erreur ... Serait-il possible d'avoir de l'aide s'il vous plait afin que je puisse terminer mon exercice et surtout savoir où j'ai commis mon erreur ?
Voici ce que j'ai déjà réalisé :
a- Coordonnées des points I, J et K
A(0;0;0) B(1;0;0) D(0;1;0) S(0;0;1) C(1;1;0)
AI=1/2AB alors I(1/2;0;0)
AJ=1/2AD alors J(0;1/2;0)
K milieu de [SC] et SC(1;1;-1) donc SK=1/2SC alors K(1/2;1/2;-1/2)
b- Equation du plan (IJK)
IJ(-1/2;1/2;0) IK(0;1/2;-1/2)
Il n'existe pas de réel k tq IJ=kIK
donc IJ et IK non colinéaires donc I, J et K non alignés et définissent un plan
n normal à (IJK) 
n.IJ=0 et n.IK=0
-1/2a+1/2b=0 et 1/2b-1/2c=0
-1/2a=-1/2b et -1/2c=-1/2b
On prend b=-2
-1/2a=1 et -1/2c=1
a=-2 ; b=-2 ; c=-2
donc n(-2;-2;-2) normal à (IJK)
M(x;y;z) 
(IJK) IM.n=0
-2(x-1/2)-2(y-0)-2(z-0)=0
-2x-2y-2z+1=0
Equation cartésienne de (IJK) : -2x-2y-2z+1=0
c- Représentation paramétrique de (SB)
B(1;0;0) S(0;0;1)
SB(1;0;1) vecteur directeur de (SB)
M(x;y;z) un point de l'espace
M(SB) BM et SB colinéaires
t 
tq BM=tSB
t tq x=1+t / y=0 / z=-t
Donc D : x=1+t / y=0 / z=-t
d- Coordonnées du point N
n(-2;-2;-2) vecteur normal à (IJK)
u(1;0;-1) vecteur directeur de (SB)
u.n=1*(-2)+0*(-2)-1*(2)=0
Et là je bloque puisque je trouve que les vecteurs sont orthogonaux et que donc le plan et la droite sont parallèles et ils le sont même strictement car les coordonnées d'un point de (SB) ne vérifient pas l'équation du plan .
Merci d'avance de m'accorder un peu de votre temps pour me permettre de réussir cet exercice
Bonjour,
K milieu de [SC] et SC(1;1;-1) donc SK=1/2SC alors K(1/2;1/2;-1/2)
ou tout simplement:
z_K=z1/2(z_S+zC)=1/2(1+0)=1/2[/tex]
remarque K est au dessus du plan ABC donc zK>0
Bonjour,
un simple croquis éviterait ce genre d'erreur sur les signes de coordonnées 
plus élaboré, on peut faire une véritable épure qui donne entièrement des conjectures quantitatives (qu'il s'agit alors de vérifier par le calcul)
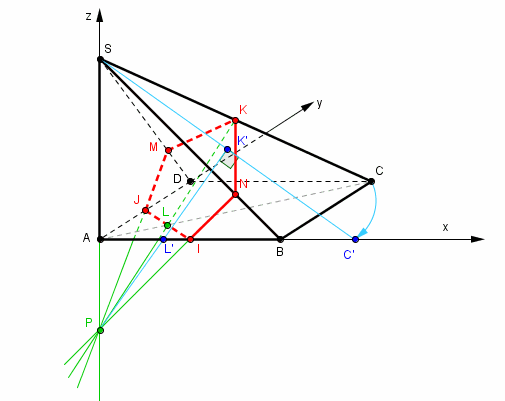
en vert la construction géométrique des points M et N et donc la conjecture que SN = (3/4)SB
on peut le démontrer sur cette figure par application du théorème de Ceva, mais ici c'est hors sujet.
par contre cela permet de vérifier qu'on ne s'est pas "grossièrement planté" dans ses calculs avec des coordonnées.
En bleu on effectue un rabattement du plan SAC sur le plan frontal SAB, qui permet de construire en vraie grandeur ce triangle SAC (SAC') et d'observer (conjecturer) que (SC) est orthogonale au plan (IJK)
par conséquent un vecteur normal au plan (IJK) devrait être colinéaire au vecteur SC ...
Nota :
1) tu n'as jamais défini ici les points M et N, on ne peut que deviner, je pense ne pas m'être trompé dans cette "divination"
2) la propriété SN = (3/4)SB est indépendante de AS = AB
par contre les calculs effectués (vecteur orthogonal) nécessitent que le repère soit orthonormé
la méthode algébrique par l'équation de plan via un vecteur normal n'est donc valable que dans ce cas très particulier où SAB et SAD sont des triangles rectangles isocèles (hauteur = côté)
Pour obtenir l'équation du plan (IJK) dans un repère non orthonormé, la notion de vecteur normal n'existe pas.
on peut par contre écrire que ce plan passe par I, J et K ce qui permet d'en obtenir l'équation directement sous la forme
ax + by + cz = 1
et on cherche a, b, c (= 1 car il est "évident" que l'origine A n'appartient pas à ce plan, sinon = d et on obtient l'équation "à un facteur près")
et permet donc de généraliser les calculs effectués via les coordonnées au cas d'une pyramide quelconque.
Merci beaucoup pour vos réponses et explications qui m'ont permis de terminer cet exercice !
a- Coordonnées des point I, J et K
I(1/2;0;0) J(0;1/2;0) K(1/2;1/2;1/2)
b- Equation du plan (IJK) : 2x+2y-2z-1=0
c- Représentation paramétrique de (SB)
x=t / y=0 / Z+1-t ; t
d- Coordonnées point N : N(3/4;0;1/4) d'où BN=1/4BS
e- Position de P sur [SD]
Représentation paramétrique de (SD) : x=0 / y=t / z=1-t ; t
Coordonnées de P : P(0;3/4;1/4) d'où DP=1/4DS
Encore merci pour toutes vos explications !
Annuler
connectez vous