Inscription / Connexion Nouveau Sujet
Racine Carrée
Bonjour à tous j'aimerais avoir de l'aide pour mon DM de mathématiques car je ne comprend pas du tous, j'ai essayé de chercher. Cordialement.
I/ La fonction racine carrée.
Le plan est muni d'un repère orthonormé (o, 
)
1)Construction géométrique de la courbe.
Considérons sur l'axe des abscisses un point N de coordonnées (x,0), x étant un réel strictement supérieur à 0. On appelle N' l'image de N dans la translation de vecteur
a) Représenter les points N et N'
b) Construire ensuite le point , de même abscisse x que N, d'ordonnée y positive et tel que le triangle OMN' soit rectangle en M. Expliquer la construction.
c) Montrer que MN=
x en utilisant le théorème de Pythagore.
d) Construire de la même façon 10 points de la courbe d'équation y=x
2)Etude de la fonction racine carrée.
Soit f la fonnction f:x
x définie sur lintervalle [0;+ l'infinie [
a) a et b étant deux réels positifs, développer ( b- a)( b+a)
b) En déduire que si 0
a<b alors ab
c) Que peut-on dire du sens de variation de f ?
3) Lien avec la courbe de la fonction carré.
a) Tracer la droite d'équation y=x
b) Tracer l'image des 10 points obtenus en 1)d) par la symétrie orthogonale d'axe
c) Montrer que ces images appartiennent à la courbe d'équation y=x²
On admet alors que les fonctions carré et raciine carré, sur 0;+ l'infinie[ sont symétriques par rapport à la droite d'équations y=x
Merci de m'aider car je trouve ce DM vraiùment dur.
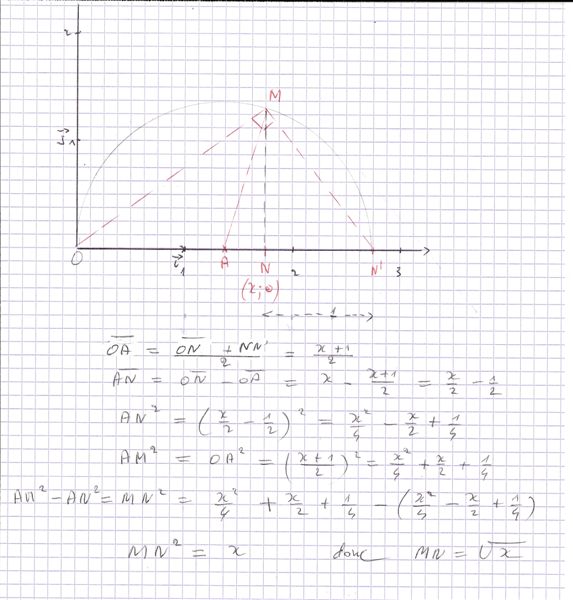
Donc on place N(x;0) puis N' tel que le vecteur NN'(1;0).
Il faut tracer le cercle de diamètre [ON'] pour construire le triangle OMN' rectangle en M.
Donc son centre est le pont A de ma figure avec A milieu de [ON'].
OK ?
Ensuite dans les calculs faits ci-dessus , je raisonne en mesures algébriques tant que je n'élève pas au carré car le point N peut avoir une abscisse < 1 , ce qui n'est pas le cas dans ma figure.
Mais même si l'abscisse de N < 1 , on aura toujours les mêmes mesures algébriques.
Quand on élève au carré , il n'y a plus de soucis.
Bien sûr , tu as compris que j'ai utilisé Pythagore dans le triangle ANM rectangle en N.
d) Construire de la même façon 10 points de la courbe d'équation y=x
Alors là, bon courage !! Cela va être un "fouillis" pas possible !!
Moi, j'ai pris une unité = 4 cm sur les axes. Il faut peut-être prendre :
1 unité = 10 cm
pour éviter le "fouillis" !!
2)
Pour aller plus vite : V sera le symbole de la racine carrée. OK ?
a)
(Va-Vb)(Va+Vb)=...- ...
car tu reconnais une identité remarquable bien connue.
b)
On sait que a < b avec a et b tous deux positifs.
On peut donc élever au carré sans changer le sens de l'inégalité car la fct carrée est croissante sur [0;+inf[, ce qui donne :
a² < b²
soit :
b² -a² > 0
soit
(Vb-Va)(Vb+Va) > 0
Mais le facteur (Vb+Va) est positif donc le produit positif implique :
Vb-Va > 0
soit :
Va < Vb
Donc
si 0 a < b alors a < b
c) On sait que :
f est strictement croissante si pour a < b dans un intervalle donné on a f(a) < f(b) .
3)
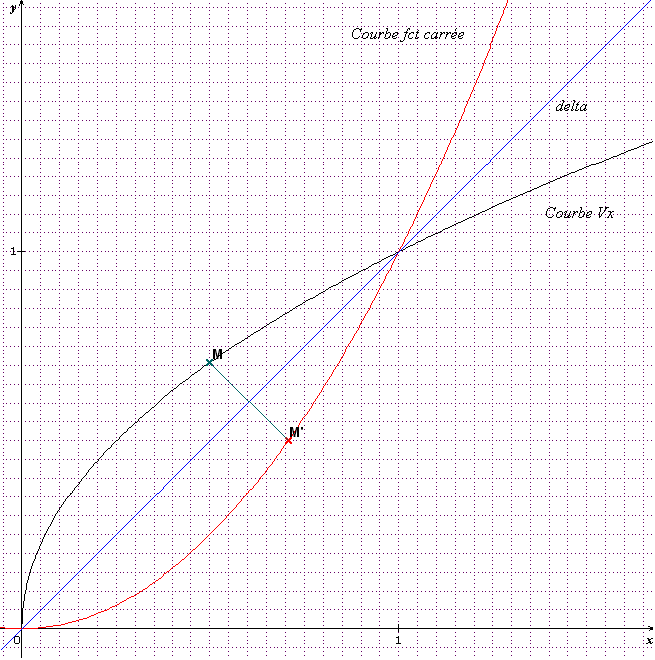
a) b ) Bon courage : je t'ai fait le sym d'un point quelcomque M par la symétrie orthogonale d'axe pour obtenir M'.
Donc (MM') 
et coupe [MM'] en son milieu.
c)
Tu vas appliquer ce qui suit que tu es censé(e) savoir je suppose :
Le symétrique d'un point de coordonnées (x;y) par rapport à la première bissectrice( qui est la droite ) est (y;x).
Donc M(x;Vx) a pour sym par rapport à le point M'(Vx;x).
L'ordonnée de M' est x et son abscisse Vx .
Donc yM'=(xM')² car x=(Vx)²
Donc M' est sur la courbe d'équation y=x²
Bonjour, merci beaucoup de vous avoir donner la peine de bien vouloir me répondre avec pas mal de précisions 
Je vais regarder ça plus en détail et vous reposez éventuellement des questions si je ne comprend pas.
Annuler
connectez vous