Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... LicenceMaths 2e/3e a AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques
Niveau LicenceMaths 2e/3e a
Partager :

Raisonnement par récurrence

Posté par
Foxdevil 30-07-20 à 23:23

Salut ,

Quand on fait un raisonnement par récurrence, en général, l'initialisation est assez simple (pour ne pas dire simpliste).
Je cherche un exemple de démonstration par récurrence où au contraire, l'hérédité est beaucoup plus facile que l'initialisation. Et donc, où on sue pour initialiser la propriété.

Il me semblait en avoir croisé une il y a quelques années mais je n'arrive pas à la retrouver d'ou ma demande

C'est peu être facile, mais ça ne me saute pas aux yeux

Merci

Posté par
lionel52re : Raisonnement par récurrence 31-07-20 à 09:27

Hello!

Exemple : lemme des noyaux

Posté par
carpediemre : Raisonnement par récurrence 31-07-20 à 13:39

salut

l'initialisation est toujours simple quand on donne le rang de départ ...

tu connais les exo classiques : montrer que 2^n \ge n^2 à partir du rang ... (qui est toujours donné au lycée)

mais si je te pose le pb sous la forme : pour quels entiers n a-t-on 2^n \ge n ? comment fais-tu ?

PS : l'exemple est ici trivial et archi-classique mais c'est pour te donner une idée du pb : en gros : on "sait" (ou on démontre que) que la propriété est héréditaire ... mais à partir de quand ??

Posté par
carpediemre : Raisonnement par récurrence 31-07-20 à 13:44

salut

l'initialisation est toujours simple quand on donne le rang de départ ...

tu connais les exo classiques : montrer que 2^n \ge n^2 à partir du rang ... (qui est toujours donné au lycée)

mais si je te pose le pb sous la forme : pour quels entiers n a-t-on 2^n \ge n{\red ^2} ? comment fais-tu ?

PS : l'exemple est ici trivial et archi-classique mais c'est pour te donner une idée du pb : en gros : on "sait" (ou on démontre que) que la propriété est héréditaire ... mais à partir de quand ??

ainsi par exemple et si je te mets n^{10} ou n'importe quel exposant ...
on sait qu'une exponentielle l'emporte sur la puissance à l'infini ... mais à partir de quand est-ce vrai ?

d'ailleurs le raisonnement par récurrence fera intervenir des conditions fort probablement suffisantes (dès que l'exposant n'est plus 2 ou 3) et ne donnera peut-être pas le rang minimal mais un rang à partir duquel la propriété est héréditaire ...
et pour trouver le rang minimal ... ben bonjour !!! ou alors utiliser un algo pour traiter tous les cas (en nombre fini) restants ...

Posté par
mousse42re : Raisonnement par récurrence 31-07-20 à 16:02

Salut,

carpediem, peux-tu faire tourner ton algo là-dessus

P(n):9\mid(10^n+1)

Posté par
lafol Moderateurre : Raisonnement par récurrence 31-07-20 à 16:11

Bonjour
pas besoin d'une récurrence pour voir que 10^n+1 est congru à 2 modulo 9, quelque soit n, si ?

Posté par
mousse42re : Raisonnement par récurrence 31-07-20 à 16:17

Bonjour lafol
je voulais juste taquiner carpediem, mon message est hors sujet, car il parlait du passage d'une CS à une CNS pour l'hérédité

Posté par
carpediemre : Raisonnement par récurrence 31-07-20 à 16:56

lafol : certes mais c'est une question didactique et pédagogique fondamentale (pour qui veut réellement éduquer et instruire et non pas faire réciter des math en donnant l'illusion de la réussite) sur le problème de la vérité d'une affirmation

la plupart des élèves (et bon nombre d'adultes) pensent que la proposition si deux est supérieur à trois alors les chats sont verts est fausse (l'implication est vraie)

et si on considère les propositions P(n)  : 9 $  divise $ 10^n + 1  et  Q(n)  :  9 $ divise $ 10^n - 1 il est intéressant de comprendre que ces deux propriétés sont héréditaires : les implications P(n) => P(n + 1) et Q(n) => Q(n + 1) sont vraie

pourtant 'une des propriétés est fausses pour tout n et l'autre est vraie pour tout n ...

et pour poursuivre avec mousse42 : il n'y a pas de pb puisque la propriété est héréditaire pour tout n ... or P(0) est faux ... donc c'est terminé !!!

et pas besoin d'algo !!! qui ne sera nécessaire que lorsqu'on montre qu'une propriété est héréditaire à partir d'un certain rang ... mais qui peut-être vraie avant ce rang sans que la récurrence puisse le montrer ou parce qu'on a travaillé par condition suffisante ...

c'est plutôt le pb "à l'envers" qui ... pose pb : c'est quand on démontre qu'une propriété est héréditaire à partir d'un rang n mais qu'elle est vraie qu'à partir d'un rang m > n

et là pour trouver ce rang m ben ça peut être problématique ...

visualisation (avec n = 10 pour simplifier) 

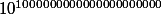P(0) => P(1) => P(2) => .... => P(9) => P(10) => P(11) => .... => P(10^{10000000000000000000000000000} - 1) => P(10^{1000000000000000000000} => ...


et l'implication P(n) => P(n + 1) est fausse jusqu'à 9 et vraie à partir du rang 10 mais la propriété P(n) n'est vraie qu'à partir du rang 10^{1000000000000000000} ...
et pourtant toutes mes implications sont vraies puisque les implications F => F et F => V sont vraies

ben faut aller le chercher ce nombre ... surtout si on n'est pas sûr que ce soit vraie à un rang donné ... auquel cas l'algo tournera indéfiniment ...

Posté par
mousse42re : Raisonnement par récurrence 31-07-20 à 17:06

carpediem

et pour poursuivre avec mousse42 : il n'y a pas de pb puisque la propriété est héréditaire pour tout n ... or P(0) est faux ... donc c'est terminé !!!


Il me semble que "P(0) est faux" n'est pas suffisant.

Posté par
mousse42re : Raisonnement par récurrence 31-07-20 à 19:40

Foxdevil @ 30-07-2020 à 23:23

Salut ,

Quand on fait un raisonnement par récurrence, en général, l'initialisation est assez simple (pour ne pas dire simpliste).
Je cherche un exemple de démonstration par récurrence où au contraire, l'hérédité est beaucoup plus facile que l'initialisation. Et donc, où on sue pour initialiser la propriété.

Il me semblait en avoir croisé une il y a quelques années mais je n'arrive pas à la retrouver d'ou ma demande

C'est peu être facile, mais ça ne me saute pas aux yeux

Merci



Je reviens à la question initiale, en fouillant sur le net, j'ai trouvé :

P(n) : toute suites bornée dans \R^n possède une sous-suite qui converge

Posté par
carpediemre : Raisonnement par récurrence 31-07-20 à 19:42

ouais en fait tu as raison ... que ce soit 0 ou un entier quelconque ...on est dans la mede !!!

Posté par
Foxdevilre : Raisonnement par récurrence 31-07-20 à 22:29

Salut à tous,

Merci beaucoup pour vos réponses!


lionel52 @ 31-07-2020 à 09:27

Hello!

Exemple : lemme des noyaux
L'exemple m'a l'air vraiment pas mal! L'hérédité est un jeu d'enfant, car il suffit de former n polynômes (dont l'un sera le produit des deux derniers par exemple) à partir des n+1 et appliquer l'HR aux n polynômes (qui seront toujours premiers deux à deux) ainsi qu'au dernier (le produit donc).
Mais pour l'initialiser, on doit le prouver pour n=2. Et c'est moins évident à priori...

carpediem @ 31-07-2020 à 13:39

l'initialisation est toujours simple quand on donne le rang de départ ...
hé bien non justement!

L'idée ici c'est d'avoir une propriété difficile à montrer pour n=0 ou 1 (ou peu importe le début), mais facilement transmissible...

carpediem

et pour poursuivre avec mousse42 : il n'y a pas de pb puisque la propriété est héréditaire pour tout n ... or P(0) est faux ... donc c'est terminé !!!


mousse42 @ 31-07-2020 à 17:06

Il me semble que "P(0) est faux" n'est pas suffisant.
Oui, ça ne fait que décaler le problème d'un cran. A priori, il faudrait montrer que P(n) est faux encore pour....bah pour tout n plus grand que 1 non?

mousse42 @ 31-07-2020 à 19:40

Je reviens à la question initiale, en fouillant sur le net, j'ai trouvé :

P(n) : toute suites bornée dans \R^n possède une sous-suite qui converge
Oui, là aussi ça m'a l'air vraiment pas mal!
La propriété se transmet facilement car en s'y prenant bien on considère juste le n-uplet et on applique l'HR au n-uplet et la suite seule pour prouver la propriété au rang n+1.
Mais pour n=1, c'est Bolzano-W qui est un peu moins easy à la main.

Dans le même style du coup on a la complétude de \mathbb{R}^n, où l'hérédité se prouve en considérant un n-uplet qui sera nécessairement de Cauchy, etc...l'initialisation est pas ouf monstrueuse; mais quand même un peu moins facile que l'hérédité.

Posté par
Foxdevilre : Raisonnement par récurrence 31-07-20 à 22:42

mousse42 @ 31-07-2020 à 19:40

Je reviens à la question initiale, en fouillant sur le net, j'ai trouvé :

P(n) : toute suites bornée dans \R^n possède une sous-suite qui converge
Tu as tapé quoi pour trouver cet exemple?

carpediem

PS : l'exemple est ici trivial et archi-classique mais c'est pour te donner une idée du pb : en gros : on "sait" (ou on démontre que) que la propriété est héréditaire ... mais à partir de quand ??

ainsi par exemple et si je te mets n^{10} ou n'importe quel exposant ...
on sait qu'une exponentielle l'emporte sur la puissance à l'infini ... mais à partir de quand est-ce vrai ?

d'ailleurs le raisonnement par récurrence fera intervenir des conditions fort probablement suffisantes (dès que l'exposant n'est plus 2 ou 3) et ne donnera peut-être pas le rang minimal mais un rang à partir duquel la propriété est héréditaire ...
et pour trouver le rang minimal ... ben bonjour !!! ou alors utiliser un algo pour traiter tous les cas (en nombre fini) restants ...
Oui, c'est sûr. C'est un problème assez indépendant de la récurrence il me semble d'ailleurs. Et globalement assez difficile.
Il y a surement d'autres exemples plus simple, mais celui qui me vient en tête est la conjecture de Poincaré qui a été démontré (je ne sais pas si c'était une récurrence d'ailleurs ) pour tout n plus grand que 7, puis à la main pour les valeurs restantes...

Posté par
mousse42re : Raisonnement par récurrence 31-07-20 à 22:51

Salut

J'ai tapé :"induction with difficult base case"

Posté par
carpediemre : Raisonnement par récurrence 31-07-20 à 23:20

Foxdevil @ 31-07-2020 à 22:29

Citation :
Exemple : lemme des noyaux
L'exemple m'a l'air vraiment pas mal! L'hérédité est un jeu d'enfant, car il suffit de former n polynômes (dont l'un sera le produit des deux derniers par exemple) à partir des n+1 et appliquer l'HR aux n polynômes (qui seront toujours premiers deux à deux) ainsi qu'au dernier (le produit donc).
Mais pour l'initialiser, on doit le prouver pour n=2. Et c'est moins évident à priori...
il y a de nombreux exemples ou l'hérédité consiste à prouver l'initialisation et qui peut-être plus ou moins facile

un exemple classique de niveau lycée basé sur le même principe que le lemme des noyaux (globalement plus facile tout de même) : la dérivée d'un produit de n fonctions : une fois qu'on a démontré la dérivée du produit de deux fonctions alors l'hérédité est élémentaire

de même le lemme de Gauss : si p est premier et divise ab alors p divise a ou p divise b se généralise immédiatement à un produit de n facteurs par récurrence .... une fois qu'on a fait l'initialisation ...

Posté par
mousse42re : Raisonnement par récurrence 31-07-20 à 23:37

Salut

Pour l'exemple de P(n):\,2^n\ge 10^n

L'hérédité est vraie à partir de n=14 mais pour l'initialisation il faut attendre n=59,

Posté par
mousse42re : Raisonnement par récurrence 31-07-20 à 23:39

mousse42 @ 31-07-2020 à 23:37

Salut

Pour l'exemple de P(n):\,2^n\ge 10^n

L'hérédité est vraie à partir de n=14 mais pour l'initialisation il faut attendre n=59,


Je rectifie, il suffit que n\ge 14 pour que l'hérédité soit vraie, ...

Posté par
mousse42re : Raisonnement par récurrence 31-07-20 à 23:43

c'est P(n) :2^n\ge n^{10} bien sûr

Posté par
Foxdevilre : Raisonnement par récurrence 31-07-20 à 23:50

mousse42 @ 31-07-2020 à 22:51

J'ai tapé :"induction with difficult base case"
Merci! J'aurais dû/pu y penser! 🤦‍♂️ Pas encore le réflexe de systématiquement chercher en anglais (le pire c'est que pour certaines questions mathématiques, je le fais )....alors que c'est beaucoup plus riche et intéressant!

carpediem @ 31-07-2020 à 23:20

un exemple classique de niveau lycée basé sur le même principe que le lemme des noyaux (globalement plus facile tout de même) : la dérivée d'un produit de n fonctions : une fois qu'on a démontré la dérivée du produit de deux fonctions alors l'hérédité est élémentaire

de même le lemme de Gauss : si p est premier et divise ab alors p divise a ou p divise b se généralise immédiatement à un produit de n facteurs par récurrence .... une fois qu'on a fait l'initialisation ...
carrément! (je suis justement tombé sur le 1er que tu cites en cherchant ce qu'a proposé mousse42 ) Merci aussi pour l'autre!

Dans le même style, je suis tombé aussi sur Taylor avec reste intégral. L'hérédité est facile (simple IPP), mais le cas de base (n=1) est (en fonction des hypothèses qu'on s'autorise) archi non trivial: le Théorème fondamental de l'analyse

mousse42 @ 31-07-2020 à 23:37

Salut

Pour l'exemple de P(n):\,2^n\ge 10^n

L'hérédité est vraie à partir de n=14 mais pour l'initialisation il faut attendre n=59,
pas compris

Posté par
Foxdevilre : Raisonnement par récurrence 31-07-20 à 23:50

mousse42 @ 31-07-2020 à 23:43

c'est P(n) :2^n\ge n^{10} bien sûr
ahhhhhh ok

Posté par
carpediemre : Raisonnement par récurrence 01-08-20 à 11:54

ha oui Taylor est aussi un classique du genre : l'initialisation est pénible ... mais ensuite ça roule tout seul par IPP ...

Posté par
verdurinre : Raisonnement par récurrence 01-08-20 à 20:28

Bonsoir,

Citation :
P(n) : toute suite bornée dans \R^n possède une sous-suite qui converge

Il y a quand même des démonstrations sans récurrence qui ont exactement le même niveau de complexité que la démonstration de P(1) : toute suite dans un compact admet au moins une valeur d'adhérence.


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1674 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !