Inscription / Connexion Nouveau Sujet
Recherche d une fonction mathématique en informatique de gestion
Bonjour à tous,
Je suis très impressionné par le nombre de sujets de ce forum, et par la qualité des réponses qui y sont formulées. Bravo à tous les intervenants !
Je vous expose mon problème dans le détail pour le rendre plus concret (et aussi montrer que les maths ne sont uniquement destinées aux disciplines scientifiques mais sont utiles dans beaucoup de métiers, pour ceux qui n'en seraient pas encore convaincus...)
Je suis informaticien de gestion. Dans le cadre de mes activités professionnelles, je suis en train de construire une méthode qui permet d'apprécier la qualité des programmes informatiques. Pour celà, chaque programme est évalué par un outil qui fournit trois mesures reflétant la qualité du programme, chacune correspondant à un critère qualité différent. Chaque mesure est un nombre entier supérieur ou égal à 1, munie d'un seuil. Lorsque la mesure est inférieure ou égale au seuil, la qualité du programme est bonne, plus elle le dépasse plus la qualité est mauvaise. J'utilise ces 3 mesures dans une moyenne pondérée afin d'obtenir une valeur unique pour qualifier la qualité du programme, ce qui me donne de bons résultats.
Toutefois, certains types de programmes ne sont pas évalués correctement par cette méthode et, pour ceux-là, je dois m'y prendre autrement. J'ai choisi de pondérer la valeur de deux des mesures par la troisième (appelons-la x). Mais cette pondération n'est pas linéaire. C'est là que débutent mes problèmes... (il faut dire que mon dernier cours de maths remonte à 25 ans)
Le coefficient de pondération f est une fonction de x dont je fixe les conditions comme suit :
a) f(x) est définie et continue au moins sur [1, +oo[
b) f(x) est croissante sur [1, +oo[
c) f(1) = 0
d) f(s) > 1/2
e) lim f(x) = 1
x -> +oo
f) f'(1) = 0
g) f'(s) = +oo ; s est le seuil dont j'ai parlé plus haut
Voici ce que celà donnerait selon moi (je ne suis pas sûr que la condition g) corresponde bien au dessin).
J'avais trouvé une fonction intéressant (moyennant changements d'échelle et de repère) avec f(x) = x / (|x| + 1) ; |x| : valeur absolue de x. Mais le point d'inflexion ne me convient pas car f'(x) = 1 en ce point.
Quelqu'un peut-il m'aider ?
Merci d'avance (au moins pour avoir eu la patience d'arriver jusqu'à cette ligne-ci).
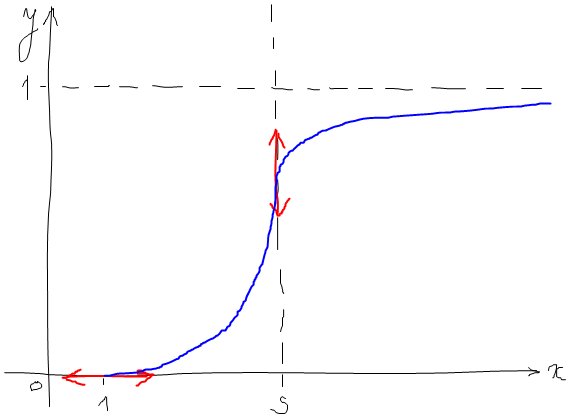
En fait, vu ta courbe, la condition g) est en fait :
* limite à gauche de f' en s = -l'infini
* limite à droite de f' en s = +l'infini
Pour obtenir une fonction qui convient, je te donne une méthode possible :
D'abord on considère la fonction définie sur
par
. Cette fonction vérifie les propriétés suivantes :
. Puis on la prolonge ("complète") sur
en "complétant" sa courbe sur
par le symétrique de la courbe sur
par rapport à l'origine du repère.
Puis il suffit d'une translation et d'un changement d'échelle pour obtenir une fonction comme tu souhaites.
stokastik :
" En fait, vu ta courbe, la condition g) est en fait :
* limite à gauche de f' en s = -l'infini
* limite à droite de f' en s = +l'infini "
C'est exactement la condition que je voulais, mais je n'avais pas su la formuler.
stokastik :
" Que vaudrait s ? "
Je n'ai pas valorisé s pour ne pas perturber le principe, mais dans le cas concret que j'ai à traiter, s = 4.
J'ai déjà pensé à utiliser deux fonctions différentes, a(x) sur ]- , 4] et b(x) sur [4, +
, 4] et b(x) sur [4, + [. Il "suffit" que les deux fonctions aient la même valeur en 4. Il n'est même pas obligatoire que la limite des dérivées en 4 soient égales à l'infini (-
[. Il "suffit" que les deux fonctions aient la même valeur en 4. Il n'est même pas obligatoire que la limite des dérivées en 4 soient égales à l'infini (- à gauche pour a'(4), +
à gauche pour a'(4), + à droite pour b'(4)
à droite pour b'(4)  ). Mais comme je pensais que des fonctions se comportant comme mon dessin étaient connues, j'avais abandonné l'idée dans l'espoir de trouver une fonction unique.
). Mais comme je pensais que des fonctions se comportant comme mon dessin étaient connues, j'avais abandonné l'idée dans l'espoir de trouver une fonction unique.
Merci quand-même pour ton aide.
Il y a certainement des formules qui donneraient cet aspect de courbe. Mais si on veut une formule unique, elle sera bien plus compliquée que si on choisi deux formules distinctes se raccordant au point (x=s ; y=ys) et présantant une continuité parfaite.
Dans ce cas, le choix est certainement assez large. Un famille de courbes qui serait un bon choix (à mon avis) est représentée sur la figure 1. (le paramètre p peut être ajusté à volonté. Par exemple pour p=2, la courbe centrale est une ellipse).
Ensuite, il suffit de faire les translations et homothéties nécessaires pour que deux des arcs de courbes se raccordent selon la forme souhaitée (voir figure 2) . C'est ce qui a été fait pour obtenir finalement les deux équations notées sur la figure 2 et qui sont les équations utilisables pour l'application pratique.
La cerise sur le gâteau : il n'est pas indispensable que les paramètres des puissances p et (1/p) soient les mêmes partout : on voit que les formules "généralisées" comportent 4 paramètres indépendants que l'on peut ajuster pour obtenir les courbures qui conviendront au mieux par rapport à la courbe souhaitée (tout en satisfaisant, dans tous les cas et sans devoir s'en préoccuper, aux diverses conditions imposées dans l'énoncé du problème). Ces diverse valeurs de p ne sont pas forcément des nombres entiers : on peut les ajuster sur les réels > 1.
J'avais subodoré qu'une fonction unique risquait d'être compliquée. Je m'étais conformé à la suggestion de stokastik et m'étais déjà orienté vers la recherche de deux fonctions ayant la même valeur en s. J'avais revu mes exigences à la baisse quant aux valeurs des dérivées en s en acceptant qu'elles soient différentes de  et même différentes d'une fonction à l'autre.
et même différentes d'une fonction à l'autre.
La famille de fonctions que tu proposes est tout à fait pertinente et répond exactement à mon problème.
Merci JJa.
PS : Je m'étais "rabattu" sur une parabole à gauche de s et sur une fonction du type à droite de s.
Certes, les fonctions que j'ai indiquées satisfont, strictement parlant, aux conditions qui étaient demandées. Mais je doute fort qu'elles soient vraiment satisfaisantes vis à vis d'autres conditions qui se présentent généralement dans les problèmes d'ajustement de courbe.
Evidemment, ne connaissant pas quelles sont les conditions subsidiaires liées à votre problème, je ne pouvais pas vous donner le conseil le plus approprié.
Par exemple, si votre problème est de faire passer une courbe au plus près d'un ensemble de points expérimentaux connus, avec les formules indiquées (ou avec beaucoup d'autres que l'on aurait pu vous proposer), il y a peu de chance que vous obteniez le meilleur résultat et vous aurez beaucoup de mal à ajuster "au mieux" les paramètres p et 1/p des formules.
Dans cette situation, un staticien vous aurait proposé une formule certainement plus pertinente qui, en plus de satisfaire aux conditions de position et de tangence aux extrémités, présenterait des facilités pour le calcul simple et rapide des paramètres d'ajustement par rapport à l'ensemble des points expérimentaux.
Il faut bien voir qu'une formule donnée un peu au hasard (et bien qu'elle convienne), ne possède pas les propriétés intrinsèques nécessaires pour pouvoir bénéficier de tout le back-ground mathématique que les statisticiens ont accumulé et qui assurent, dans la majorité des cas, des ajustements d'une précision maximum avec des calculs aussi simples que possible.


 analyse en Bts
analyse en Bts