Salut Schumi

ça a l'air d'avoir une bonne (??) tête d'espace projectif, non ? (quelle dimension ?).

Kaiser

Bonsoir,

ce problème m'intéresse alors je me permets de participer (mais je vais sûrement dire dire n'importe quoi, alors pardonnez-moi d'avance )

Il me semble que le groupe fondamental de cet espace est nul. Pourtant Kayser, l'espace auquel tu sembles penser n'a pas un groupe fondamental nul.
Ceci dit, je ne vois pas du tout à quoi cet espace peut être homéomorphe car c'est pour moi un espace de dimension 1 simplement connexe et sans bord, et ça c'est quelque chose que j'ai beaucoup de mal à imaginer...

Sauriez-vous où se situe mon erreur ?

Merci d'avance,

1emeu

Je ne pense pas que l'espace obtenu soit de dimension 1 : au départ, on a un disque qui, lui, est de dimension 2 et les points du disque ouvert ne sont pas identifiés entre eux donc on a de la dimension 2 dans le quotient.
De plus, je ne pense pas non plus que le groupe fondamental de cet espace soit nul : un lacet dans le quotient ne se relève pas forcément en un lacet sur le disque (typiquement, on peut prendre un diamètre sur le disque qui se projette en lacet). Bon, pour le côté "groupe fondamental", je ne vais pas trop m'aventurer non plus.

Bref, il me semble bien que l'on obtient le plan projectif.

kaiser

Salut !

Oui, c'est bien un plan projectif réel, ca ne fais aucun doute

Salut,

au temps pour moi, j'ai mal lu l'énoncé je croyais qu'on identifiait tous les points intérieurs du disque (ce qui donne en fait si je me trompe pas un espace topologique non séparé).

Dans le cadre de l'énoncé, c'est effectivement le plan projectif

1emeu

Waouh, zêtes kro fort. Vous avez fait comment pour trouver ça? Enfin, je veux dire qu'après coup, oui, ça a plutôt bien la tête de P²(R) mais bon pour l'imaginer... j'y aurai probablement jamais pensé!

(Donc c'est carrément homéomorphe à un "ruban de Möbius avec un couvercle": Espaces projectifs réels)

5 you.

Pour ma part, il me semble avoir déjà vu cette caractérisation du plan projectif. En fait, on peut le voir de plusieurs manières différentes :

1) en imaginant le recollement, on a, comme disait mon prof de topologie algébrique, le bec d'un oiseau qui se referme un peu bizarrement et on obtient bien la "représentation géométrique" du plan projectif.

2) on peut donner explicitement un homéomorphisme en disant qu'à un point du disque de coordonnées [a,b], on lui associe le point du plan projectif de coordonnées homogènes . Reste à vérifier que c'est bien un homéomorphisme (enfin, on sent que c'en est un mais pour le montrer, faut peut-être un peu justifier).

Kaiser

Sinon, il est aussi classique de représenter la plan projectif comme le quotient de la sphère S2, par la relation x R y si et seulement si x=+y ou -y... qu'on peut aussi voir comme étant une demi sphère (homéomorphe au disque donc) dont les points du bord diamétralement opposé sont identifié. c'est exactement ce que tu as ici.

C'est avec la caractérisation de Ksilver que j'en suis sorti. C'est comme ça qu'on a défini le plan projectif réel.

en fait, désolé, je pensais que je parlais du recollement du disque (c'est-à-dire avec ton exo), mais en fait je parlait du recollement "pratique" avec la sphère (mais bon, cela dit, la demi-sphère et le disque étant homéomorphes, c'est du pareil au même) pour obtenir le plan projectif ainsi que sa "représentation géométrique" suivante :



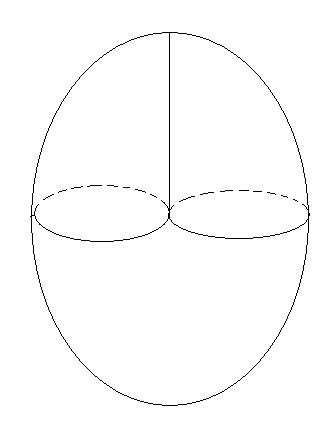
Lorsque l'on effectue le recollement avec la sphère, on a l'impression que c'est un bec d'oiseau qui se referme mais à la seule différence que la partie supérieure droite du bec se retrouve collé avec la partie inférieure gauche, et vice versa.

Kaiser