Annuler
connectez vous
trigonométrie en post-bac
- Ensemble et application Partie II
- Équations différentielles : un Cours complet avec des exemples
- Un best-of d'exos de probabilités (après le bac)
- Espaces vectoriels et Applications linéaires - supérieur
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Prepa intégrée TrigonométrieTopics traitant de trigonométrie [tout]Lister tous les topics de mathématiques
Niveau Prepa intégrée
Rectangles dans un carré
Posté par loic3544
Bonjour,
Soit un carré de côté 1. Soit un rectangle de longueur 1 et de largeur l placé à l'intérieur du carré, le long d'un bord. Soit un deuxième rectangle, identique au premier, placé "en diagonal" dans l'espace restant de manière à ce que chacun de ses coins soit en contact avec un bord de l'espace restant.
Déterminer la largeur du rectangle et l'angle formé entre la largeur du second rectangle et la base du carré .
J'arrive à obtenir une solution approchée grâce à des outils numériques mais je me retrouve toujours avec des calculs trop complexes pour conclure de manière satisfaisante.
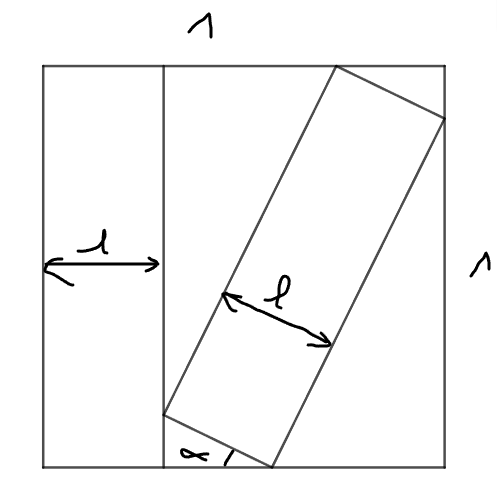
J'arrive à trouver des "formules" pour toutes les longueurs en fonction de l et 
, mais pas à les synthétiser pour obtenir une valeur exacte.
Cela vous donne deux équations à deux inconnues l et α.
On peut calculer l dans l'une et reporter dans l'autre ce qui donne une équation simple en α.
Bonjour,
Un coup de pouce avec une figure où les points sont nommés :
Les longueurs IL et LH sont des fonctions très simples de .
Comme je l'ai dit, j'ai résolu le problème numériquement, donc je sais déjà que IL et LH sont "simples".
Mais, au bout du compte, je n'arrive qu'à la relation :
l = (1-sin )/(1+ cos )
Et là, je bloque, parce que toutes les autres relations que je trouve sont triviales ou alors beaucoup trop complexes pour que j'arrive à les résoudre à la main.
Ca se trouve, c'est hyper simple, où il y a une formule trigo qui m'échappe, mais impossible d'avoir "l'illumination".
Bon, je crois que j'ai trouvé. Je ne sais pas si j'ai pas assez poussé avant où si j'ai fait une erreur de calcul qui m'a mis dedans.
J'ai noirci plusieurs pages donc je ne retrouve plus tout.
Merci !
, c'est l'horizontale DLHC qui vous la donne. Il faut faire maintenant de même avec la verticale KIL et éliminer entre les deux.
Vous avez trouvé, ?
Bonjour,
En notant et
, on obtient en considérant les deux côtés du carré le système :
On a bien sûr, en plus de la solution attendue, la solution triviale .
Bonsoir à tous,
@loic3544,
Dommage de ne pas avoir donné suite à ceci :
Citation :
Les longueurs IL et LH sont des fonctions très simples de.
En répondant par IL = cos(Les longueurs IL et LH sont des fonctions très simples de
.) et LH = sin().
On aurait su que tu démarrais bien.
Moi aussi j'ai pas mal écrit avant de trouver quelque chose de correct puis un cheminement plus "épuré".
On peut éviter les dénominateurs qui pourraient être nuls.
En reprenant les notations de GBZM, éliminer