Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Prepa intégrée AlgèbreTopics traitant de algèbre [tout]Lister tous les topics de mathématiques
Niveau Prepa intégrée
Partager :

Relation d'équivalence.

Posté par
matheux14 28-12-22 à 20:14

Bonsoir,

On dit qu'un ensemble A est dit subpotent à un ensemble B, s'il existe une injection de A dans B.

On donne X et Y deux ensembles tous deux non vides.

Existe -t-il une relation d'équivalence \mathcal{R} sur X telle que X/\mathcal{R} soit subpotent à Y ?

Une relation d'équivalence sur un ensemble E est une relation binaire ~ sur E qui est à la fois réflexive, symétrique et transitive.

Donc on suppose que notre relation \mathcal{R}' vérifie :

* Tout élément de X est \mathcal{R}'-relié à lui-même c'est-à-dire que \forall a \in X,~~ a \mathcal{R}' a.

* La relation \mathcal{R}' vérifie \forall a, b \in X, ~~a \mathcal{R}' b \Longrightarrow b \mathcal{R}' a. (ou encore, si elle est égale à sa relation réciproque.)

*  La relation \mathcal{R}' vérifie également \forall a, b, c \in X, ~~ (a \mathcal{R}' b \wedge b \mathcal{R}' c) \Longrightarrow a \mathcal{R}' c.

Je ne vois pas comment vérifier s'il existe ou pas une relation d'équivalence \mathcal{R} sur X telle que X/\mathcal{R} soit subpotent à Y...

Enfin j'essaie de visionner un transport de structure, histoire de morphisme et tout (peut-être faire de façon analogique. mais bon..), mais je ne vois pas grand chose.

Merci d'avance.

Posté par
carpediemre : Relation d'équivalence. 28-12-22 à 20:20

salut

je ne comprends pas ce prime à R ...

tu peux vérifier que pour tout fonction f de X dans Z la relation   x R y <=> f(x)= f(y) est une relation d'équivalence

il suffit alors de prendre pour f une fonction constante ...

Posté par
matheux14re : Relation d'équivalence. 29-12-22 à 08:24

Merci beaucoup

Posté par
carpediemre : Relation d'équivalence. 29-12-22 à 09:56

de rien

Posté par
Ulmierere : Relation d'équivalence. 29-12-22 à 10:55

Dit plus simplement, tu peux prendre pour \mathcal{R} la relation d'égalité, qui est bien une relation d'équivalence, et est telle que A = X/\mathcal{R} est un singleton.

Mais il manque la fin de l'exercice!
Pourquoi existe-t-il une injection de A dans Y ?

Posté par
Ulmierere : Relation d'équivalence. 29-12-22 à 11:36

Pas la relation d'égalité '=', je me suis mal exprimé.
Je veux dire que pour tous x,y, on a x\mathcal{R}y

Posté par
matheux14re : Relation d'équivalence. 29-12-22 à 17:43

Salut Ulmiere, la suite de l'exo ?

Pourquoi existe-t-il une injection.. ?

L'idée ici était de regrouper tous les éléments de l'ensemble de départ E qui ont la même image dans l'ensemble d'arrivée F par la fonction f de E dans F.

On crée ainsi une classe d'équivalence telle que deux éléments sont dans la même classe s'ils ont la même image.

Et c'est bien ce que nous suggère carpediem, lorsqu'il écrit

Citation :
tu peux vérifier que pour tout fonction f de X dans Z la relation   x R y <=> f(x)= f(y) est une relation d'équivalence


Pour la démonstration, il suffit de prendre f une fonction constante. Mais en vrai ça marche pour toutes les fonctions.

Soit f \in F^E

\forall x \in E, f(x) = f(x) \Longrightarrow x \mathcal{R} x

\mathcal{R} est réflexive.

* \forall (x, y) \in E, x \mathcal{R} y \Longrightarrow f(x) = f(y) \Longrightarrow f(y) = f(x) \Longrightarrow y \mathcal{R} x

\mathcal{R} est symétrique.

* \forall (x, y, z) \in E, (x \mathcal{R} y \wedge y \mathcal{R} z) \Longrightarrow \begin{cases} f(x) = f(y) \\ f(y) = f(z) \end{cases} \Longrightarrow f(x) = f(z) \Longrightarrow x \mathcal{R} z.

\mathcal{R} est transitive.

Donc \forall f \in F^E, la relation   x \mathcal{R} y \Longleftrightarrow f(x)= f(y) est une relation d'équivalence.

Conclusion :

Il existe au moins une relation d'équivalence \mathcal{R} sur E telle que E/\mathcal{R}soit subpotent à F.

Posté par
matheux14re : Relation d'équivalence. 29-12-22 à 18:22

L'égalité (=) étant la relation d'équivalence la plus élémentaire dans un ensemble, on comprends qu'il Il existe au moins une relation d'équivalence \mathcal{R} telle que chaque élément de l'ensemble d'arrivée F possède au plus un antécédent par la fonction f de E dans F. (Si vous remplacez \mathcal{R} par =).

Rappel : On dit qu'un ensemble A est dit subpotent à un ensemble B, s'il existe une injection de A dans B.

Posté par
Ulmierere : Relation d'équivalence. 29-12-22 à 19:17

Oui d'accord, tu quotientes par le noyau, mais ça ne répond pas à la question.

Par exemple, si X et Y sont finis et Card(X) > Card(Y) et que je prends \mathcal{R} définie par x_1\mathcal{R} x_2 \iff x_1 = x_2 (correspond à f = id_X), Alors chaque élément est dans sa propre classe, donc Card X/\mathcal{R} = Card(X) > Card(Y)

Donc il ne peut pas exister d'injection de X/\mathcal{R} \to Y, pour ce choix de \mathcal{R}.

Si on prend f (un meilleur nom serait pi, pour cette surjection) constante, il se trouve que oui, X/\mathcal{R} s'injecte dans Y, mais ce que je te demande de montrer, c'est pourquoi une telle injection existe bel et bien.
En clair, construis-moi cette injection ! (C'est très simple hein, il y a juste un petit fait dont je veux m'assurer que tu as compris l'existence)

Posté par
matheux14re : Relation d'équivalence. 30-12-22 à 11:10

Pour une fonction constante f de X dans Y, f est toujours injective.

On regarde toujours si la constante existe ou pas de l'ensemble de départ X avant de tâcher de voir s'il a un correspondant dans l'ensemble d'arrivée Y. Prenons :

X = \boxed{\left\{\pi, 0, -1, \sqrt{3}, 4, 5, \varphi, -2\right\}} et Y = \boxed{\left\{\pi, 0, -1, \sqrt{2}, \sqrt{3}, 4, 5, -2, \pi, 4, 6, 8 \right\}}

Toutes les fonctions constantes de X sont des injections.

Posté par
matheux14re : Relation d'équivalence. 30-12-22 à 11:24

Oups, j'ai mal construire l'injection..

Quel que soit le nombre en entrée d'une fonction constante, la sortie est toujours la même.

X = \boxed{\left\{\pi, 0, -1, \sqrt{3}, \varphi\right\}} et Y = \boxed{\left\{ \sqrt{2}, 4, 5, 6, 8 \right\}}

Mais là on a l'impression que c'est pas vrai du tout..

Posté par
matheux14re : Relation d'équivalence. 30-12-22 à 11:26

Ou alors peut être qu'il faut prendre une constante qui n'est ni dans X, ni dans Y..

Posté par
Ulmierere : Relation d'équivalence. 30-12-22 à 12:47

Attention, \mathcal{R_f} est une relation entre deux points de X. f est une fonction quelconque, définie sur X et à valeurs dans n'importe quel ensemble de ton choix. Il n'y a aucune raison que ce soit X ou Y, et il n'y a aucune raison que f soit injective. Si f est constante, elle est effectivement surjective, mais pas forcément injective.


Notre injection, on ne veut pas qu'elle soit de X dans Y, mais de X/R dans Y ! C'est pas f qui doit être injective, mais un autre fonction construite à l'aide de f, appelons-la \pi, définir sur X/R et à valeurs dans Y.

Posté par
carpediemre : Relation d'équivalence. 30-12-22 à 16:48

j'ai introduit un ensemble Z à 20h20 mais nul besoin de quoi que ce soit avec l'énoncé :

matheux14 @ 28-12-2022 à 20:14

On donne X et Y deux ensembles tous deux non vides.

donc X et Y contiennent au moins un élément chacun ; notons les a et b

soit alors f la fonction f: \begin{matrix} X \to Y \\ x\mapsto b \end{matrix}
et R la relation d'équivalence définie par : x R y <=> f(x) = f(y)

alors X/R = ... ?

Posté par
matheux14re : Relation d'équivalence. 30-12-22 à 19:32

X/ \mathcal{R} = l'ensemble des partitions de X, tel que deux éléments x et y sont dans la même partitions ssi f(x) = f(y) ou encore (x et y vérifient \mathcal{R} la relation d'équivalence définie par : x \mathcal{R} y \Longleftrightarrow f(x) = f(y)).

Imaginons une application quelconque f entre l'ensemble de départ X et l'ensemble d'arrivée Y.. Une application étant une fonction qui est définie partout,

Ulmiere @ 30-12-2022 à 12:47

f est une fonction quelconque, définie sur X et à valeurs dans n'importe quel ensemble de ton choix.

on peut la construire de sorte à ce qu'elle ne soit ni injective, ni surjective..
Alors on peut identifier les éléments de l'ensemble de départ X qui ont la même image dans l'ensemble d'arrivée Y. Cela nous permettra de définir une partition de l'ensemble X telle que des éléments se retrouvent dans la même partition s'ils ont la même image.

Ces partitions permettent de définir une relation d'équivalence dont les classes d'équivalence sont les partitions qu'on vient de former. Et donc on peut associer à chaque classe, une application qui associe l'image des points qui sont dans cette classe.

On a donc construit une application qui va de X/ \mathcal{R} dans l'ensemble d'arrivée Y qui n'a pas changé. Et qui cette fois est injective.

Posté par
Ulmierere : Relation d'équivalence. 30-12-22 à 20:20

Ce que tu veux, c'est X/\mathcal{R} = \{f^{-1}(\{f(x)\})  |  x\in X\}
Et ton injection \pi : r = \{x\in X : f(x) = z\}\in X/\mathcal{R}  \longmapsto z\in f(X)

Elle est à valeurs dans f(X), qu'on peut choisir comme étant un sous-ensemble de Y si on veut.

Mais ce que j'essaie de te faire dire depuis le début (et que carpediem t'a balancé ), c'est que l'injection définie ci-dessus ne peut en être une que parce que Y est non-vides.

Si Y était vide par exemple, tu ne pourrais pas définir de fonction constante à valeurs dans Y pour définir \mathcal{R}. Le fait que f(X) ait au moins un élément est ce qui permet d'y injecter X/\mathcal{R}, qui est de cardinal 1 \leqslant \text{card}(f(X)).

Si X était vide, tu ne pourrais qu'avoir \emptyset/\mathcal{R} = \emptyset et donc une injection automatique de \emptyset dans Y, mais ça n'est pas très intéressant

Posté par
carpediemre : Relation d'équivalence. 30-12-22 à 21:47

et la réponse de matheux14 est plus du verbiage qu'autre chose ...

tu nous récites beaucoup de définitions qui n'apporte pas grand chose  et le reste est peu clair ...


on a tout simplement que X/R = {X}

soit le singleton contenant (l'ensemble) X qui est la seule et unique classe d'équivalence pour la relation R

et puisque Y \supset \{b\} donc Y \ne \O la fonction \tilde{f} : \begin{matrix} X/R = \{X\} \to Y\\ x \mapsto b \end{matrix} est trivialement injective du fait que son domaine est un singleton

Posté par
matheux14re : Relation d'équivalence. 02-01-23 à 10:29

Citation :
et la réponse de matheux14 est plus du verbiage qu'autre chose ...


Bonjour,

Peut-être qu'il manque des schémas pour expliquer ce que je disais..

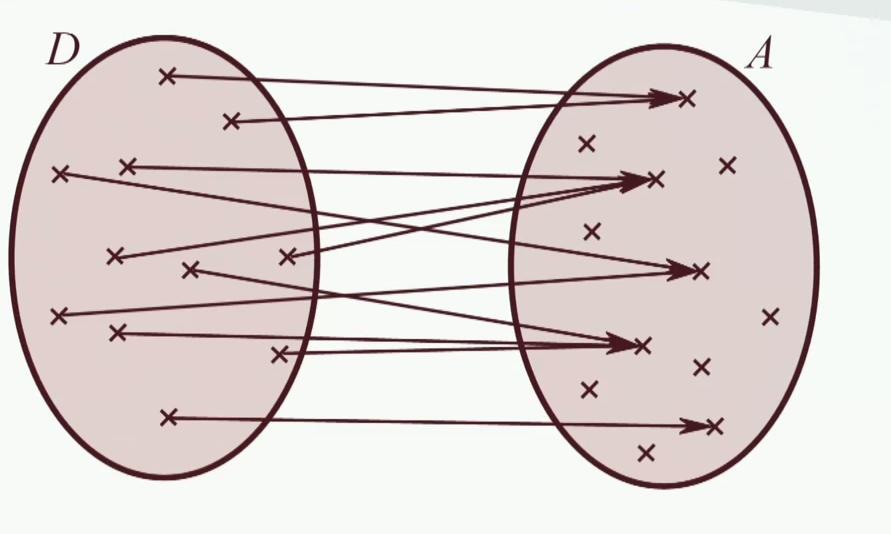
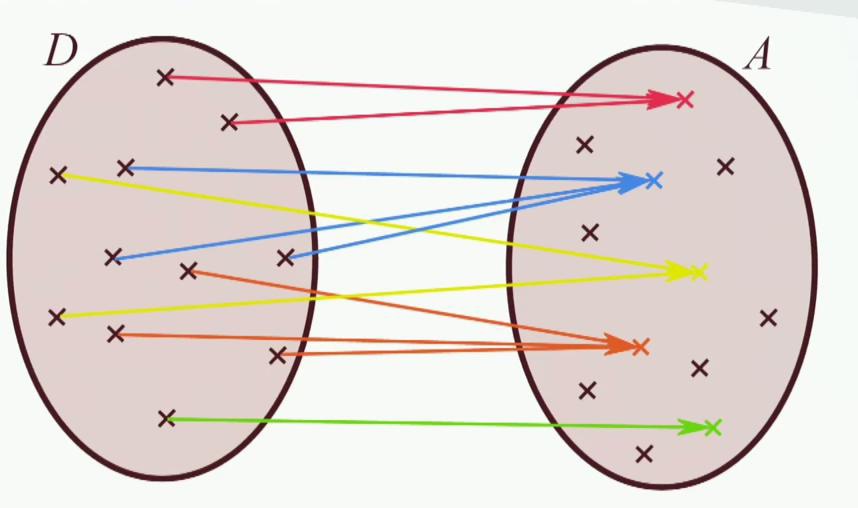
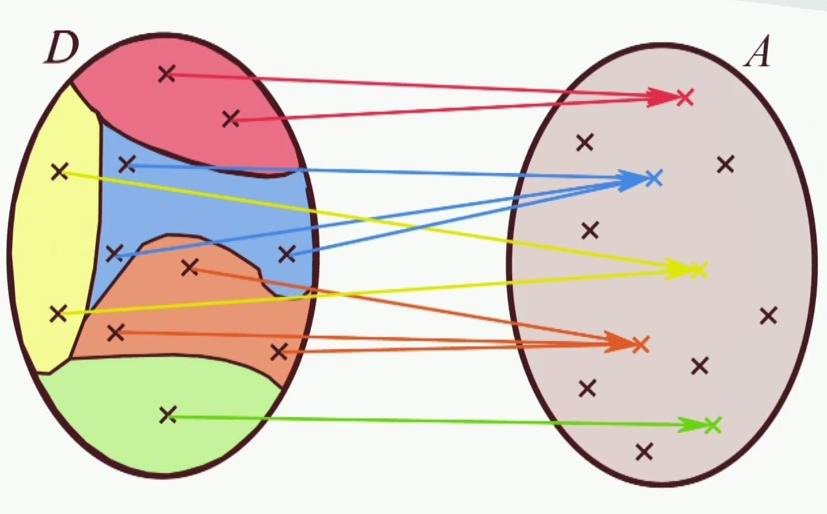
Relation d\'équivalence.

Relation d\'équivalence.

Relation d\'équivalence.

Bonne année à vous

Posté par
GBZMre : Relation d'équivalence. 02-01-23 à 12:10

Bonjour,
Oui, il est bien connu que toute application f:X\to Y se factorise en

\large X\twoheadrightarrow X/R_f \cong f(X)\rightarrowtail Y

où R_f est la relation d'équivalence associée à f.


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1674 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !