Inscription / Connexion Nouveau Sujet
Relation d'ordre (diagramme de Hasse)
Bonjour j'ai du mal à comprendre comment réaliser le diagramme de Hasse d'une relation d'ordre.
Couverture : On dit que y couvre x si x<y et s'il n'existe pas d'éléments entre eux.
Diagramme de Hasse : Si X est fini le diagramme de Hasse d'une relation d'ordre sur X est le graphe orienté dont les sommets sont les éléments de X et les arêtes (représentées du bas vers le haut) les couples (x,y) ou y couvre x.
ex : X = {a,b,c,d,e,f}
≤ = {(d,e),(d,f),(b,d),(c,d),(a,b),(a,c),(a,d),(a,e),(a,f),(b,e),(b,f),(c,e),(c,f),(a,a),(b,b),(c,c),(d,d),(e,e),(f,f)}
On a bien e qui couvre d, d qui couvre c et b qui couvre a. Or d'après le diagramme de Hasse (en pièce jointe) on aurait également f qui couvre d, d qui couvre b et c qui couvre a.
Ce que je ne comprends pas c'est que la définition nous dit que "y couvre x si x<y et s'il n'existe pas d'éléments entre eux"
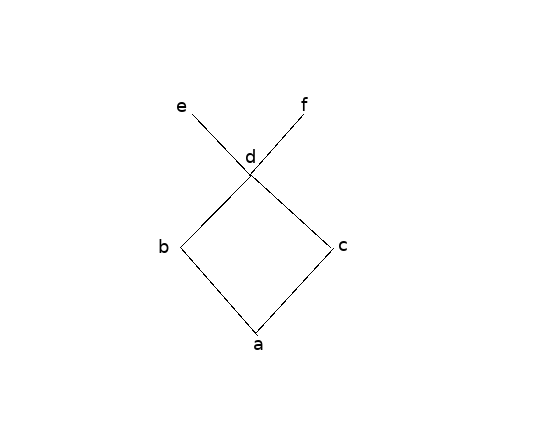
Je l'ai pas précisé mais le diagramme de Hasse qui est en pièce jointe est issu de la correction de l'exercice.
Pour résumer :
Je comprends que : e couvre d, d couvre c et b couvre a.
Je ne comprends pas que : f couvre d, d couvre b et c couvre a car comme dit précédemment (d'après la définition) y couvre x si x<y et s'il n'existe pas d'éléments entre eux
or si je prends par exemple "f qui couvre d" certes d < f mais il existe un élément entre eux c'est e
Bonjour Edison.
or si je prends par exemple "f qui couvre d" certes d < f mais il existe un élément entre eux c'est e
Non, selon le diagramme tu n'as pas d < e < f tout simplement parce que le couple (e,f) n'est pas dans ta relation d'ordre.
or si je prends par exemple "f qui couvre d" certes d < f mais il existe un élément entre eux c'est e
Bonjour !
Je ne vois pas dans la description de ton ensemble ordonné la relation
En revanche on trouve tous les autres couples (en particulier


