Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. SecondeForum de Maths Seconde TrigonométrieTopics traitant de trigonométrie [tout]Lister tous les topics de mathématiques
Niveau seconde
Partager :

relation entre le cosinus et le sinus

Posté par
adel01 18-02-12 à 02:52

bien le salut a vous

me revoila avec un nouvel exemple mais cette fois il s'agit de trigonometrie y a une relation que je voudrais comprendre :

3. D'après le théorème de Pythagore dans le triangle ONM rectangle en N, on a , ON2+NM2 = OM2et comme le cercle est de rayon 1, cela donne une relation entre cos(x) et sin(x):  
cos2 x + sin2x = 1.

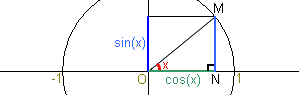
relation entre le cosinus et le sinus

Posté par
Bachstelzere : relation entre le cosinus et le sinus 18-02-12 à 02:55

Bonjour

Qu'est-ce que tu ne comprends pas ?

Posté par
adel01re : relation entre le cosinus et le sinus 18-02-12 à 03:10

le fait que l'addition  des deux au carré font 1 je parle du cos et du sin biensure.

Posté par
Bachstelzere : relation entre le cosinus et le sinus 18-02-12 à 03:12

Bah tu as la figure devant les yeux, je ne vois pas ce qu'on peut faire de plus... \cos^2x + \sin^2x = 1, c'est vrai pour tout réel x.

Posté par
Jay-MDémonstration 18-02-12 à 03:31

Bonjour.

\sin^2x + \cos^2x = \left(\sin x \right)^2 + \left(\cos x \right)^2
                           = \left(\sin \widehat{\text{MON}} \right)^2 + \left(\cos \widehat{\text{MON}} \right)^2
                           = \left(\dfrac{\text{MN}}{\text{OM}} \right)^2 + \left(\dfrac{\text{ON}}{\text{OM}} \right)^2
                           = \dfrac{\text{MN}^2}{\text{OM}^2} + \dfrac{\text{ON}^2}{\text{OM}^2}
                           = \dfrac{\text{MN}^2 + \text{ON}^2}{\text{OM}^2}
                           = \dfrac{\text{OM}^2}{\text{OM}^2}
                           = 1\text{.}
\text{Donc}\ \boxed{\sin^2x + \cos^2x = 1}\text{.}

Posté par
adel01re : relation entre le cosinus et le sinus 18-02-12 à 04:11

oui je pense avoir compris le principe .... merci jay-M

Posté par
Jay-Mre : relation entre le cosinus et le sinus 18-02-12 à 13:05

C'est la démonstration classique, la plus utilisée.
Bonne journée.

Posté par
adel01re : relation entre le cosinus et le sinus 20-02-12 à 02:27

c'est pas aussi compliqué que je ne le pensais merci tout de meme


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1760 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !