Inscription / Connexion Nouveau Sujet
Repère orthonormé
Bonjour je voudrais savoir si ce que j'ai fais est juste ou non voici l'énoncé ;
Le plan est muni d'un repère (O;I;J) d'unité le carreau
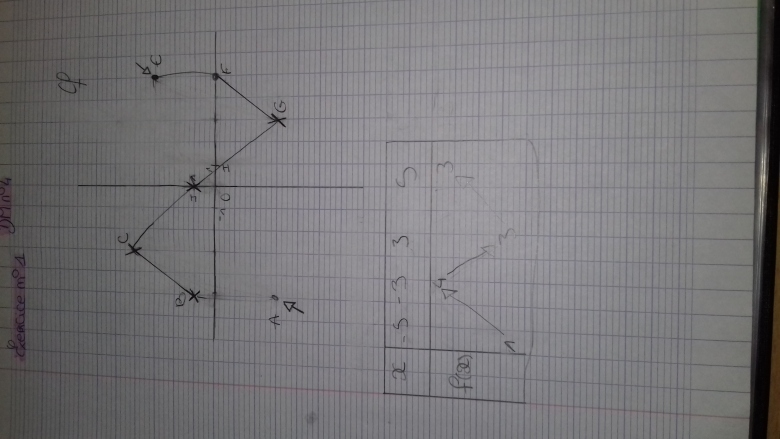
1) Tracer la courbe Cf représentative de la fonction f sachant que :
-f est définie sur [-5;5]
-le maximum de f vaut 4 et il atteint en x =-3
-le minimum de f vaut -3 et il est atteint en x=3
-f est strictement croissante sur [-5;3] et sur [3;5]
-l'image de 0 par f est 1
-0 a exactement 2 antécédents par f
2)dresser le tableau des variations de la fonction f sur l'intervalle [-5;5]
Merci à ceux quil me répondront.
bonjour
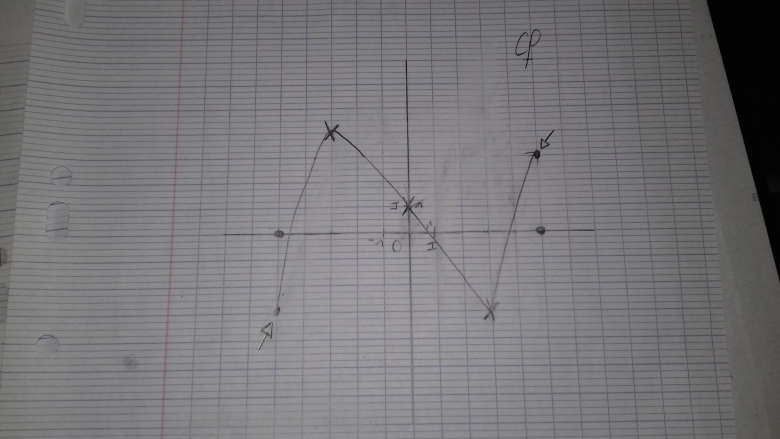
déjà il s'agit du tracé d'UNE fonction f vérifiant ces propriétés.
le 4eme renseignement est impossible tel qu'il est écrit
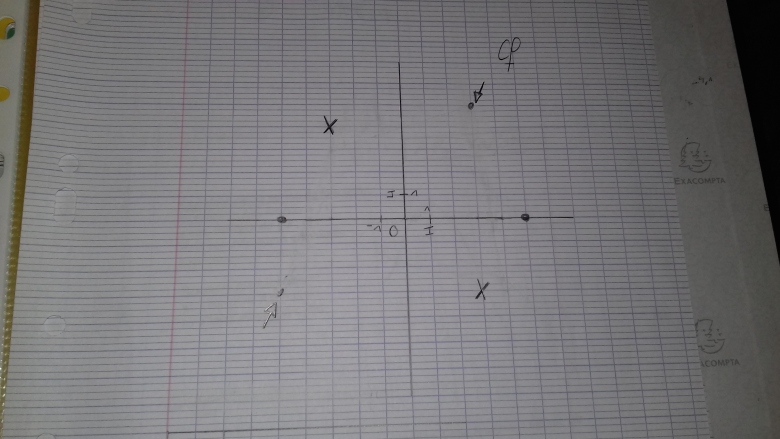
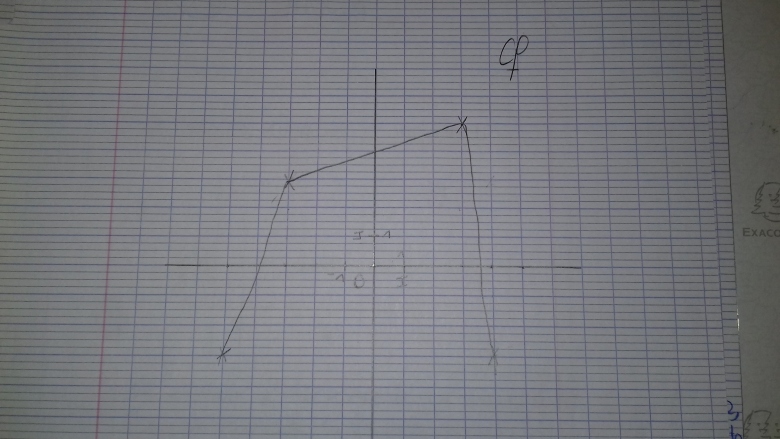
le tracé est totalement faux et ne répond pas aux renseignements 2 ; 3 ; 4 et 5
ce qui est une performance !
Bonjour
donc faux
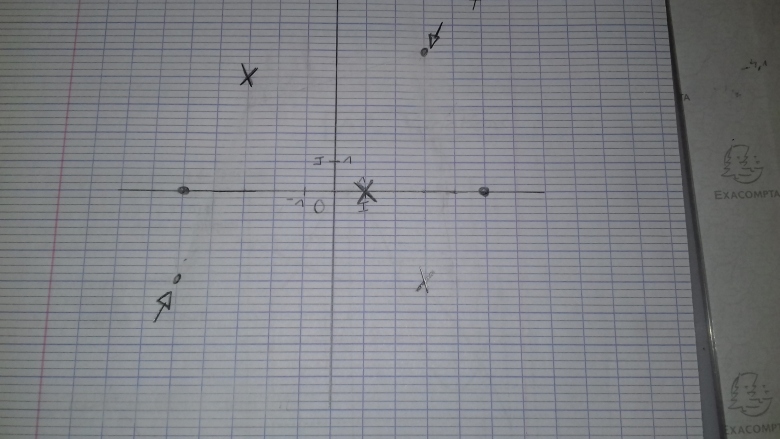
On vous dit que le maximum est atteint pour et qu'il vaut 4
pour je vois 3 et cela continue de grimper ce n'est donc pas un maximum
et comme le souligne hekla (que je salue), le renseignement 1 n'est pas respecté non plus... je l'avais zappé celui-là !
Faites un aperçu avant de renvoyer une image
si c'est celle que vous avez déjà envoyé ctrl F5
Bonjourmatheuxmatou
Pour le premier point ça passe reste bien un minimum
Pour l'autre point, non car il ne doit rien y avoir au-dessus de 4 et en outre cela ferait deux valeurs pour 3 ce qui n'est pas possible pour une fonction
Ah j'ai un beug quand j'attache la photo je la vois tel que je l'ai prise mais quand je fais l'aperçu je vois celle où il y a que le minimum et le maximun
Parce que ce devait être la précédente, d'où ma remarque
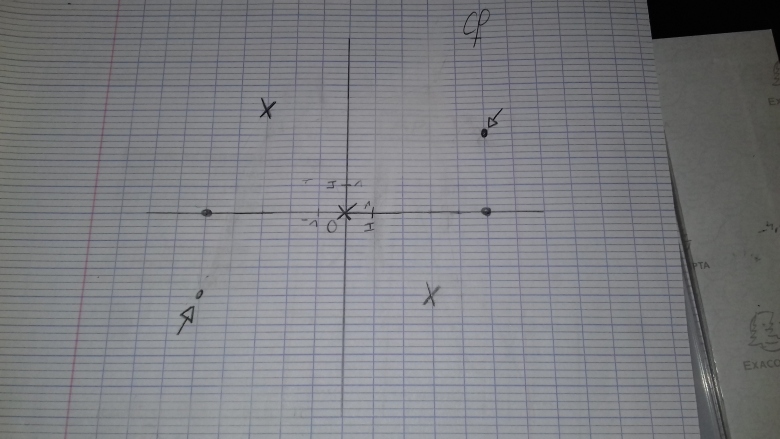
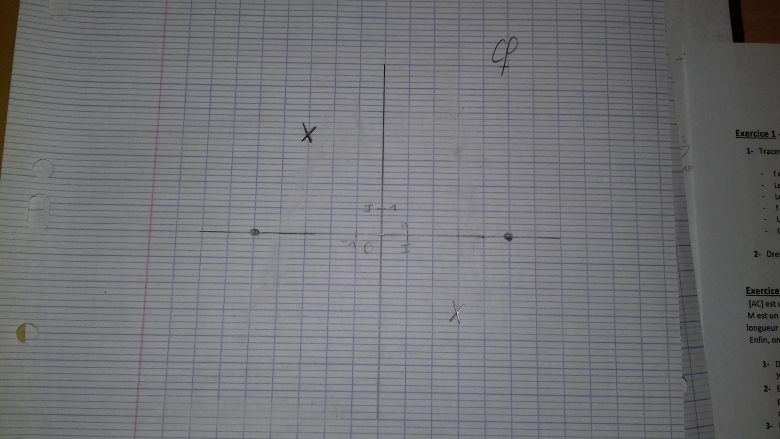
Vous pouvez placer le point tel que l'image de 0 par f est 1
Vous avez écrit que l'image de 1 est 0 alors que l'on demande que l'image de 0 soit 1
Vous confondez abscisse et ordonnée
Je vous ai dit de prendre par exemple car le point (3 ; 5) ne convient pas
La courbe ne passe pas par l'origine mais par le point de coordonnées . Après vous pourrez essayer de relier les points, non nécessairement par des segments de droites.
Non car on ne peut revenir en arrière ce qui donnerait 2 images pour une valeur en plus cela ne respecte pas les intervalles où la fonction est strictement croissante.
Continuez à descendre jusqu'au point marqué d'une croix. Et ce sera correct en laissant les autres tracés en place.
Bonjour,
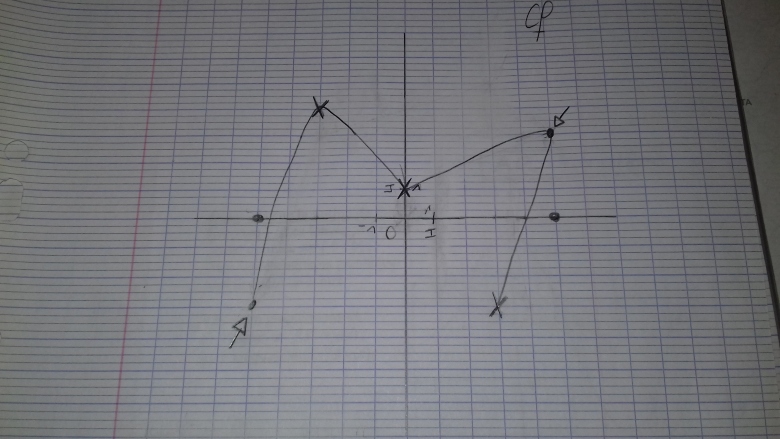
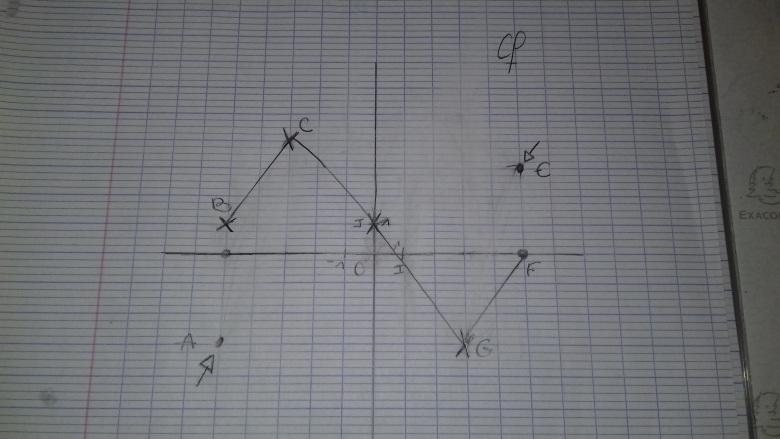
et aussi : le point à gauche ne me semble pas bon car il y aurait deux minimums :
celui en (-5; -3) de ce point là et celui en (3; -3) de l'énoncé
l'énoncé dit le minimum, il ne doit donc y en avoir qu'un seul
le point d'abscisse -5 doit être un peu remonté pour que son ordonnée soit > -3 (mais <0  )
)
nota : "jusqu'au point marqué d'une croix"
la description serait plus précise si Cosma avait mis des noms sur ses points ...
PS : (mais <0 ) supprimer cette contrainte
à voir avec la condition "-0 a exactement 2 antécédents par f" et ce qu'on fait à droite.
D'accord donc à gauche je ne change rien car "0 à exactement 2 antécédents par f "
Mais à droite je ne comprend ce qu'il faut changer
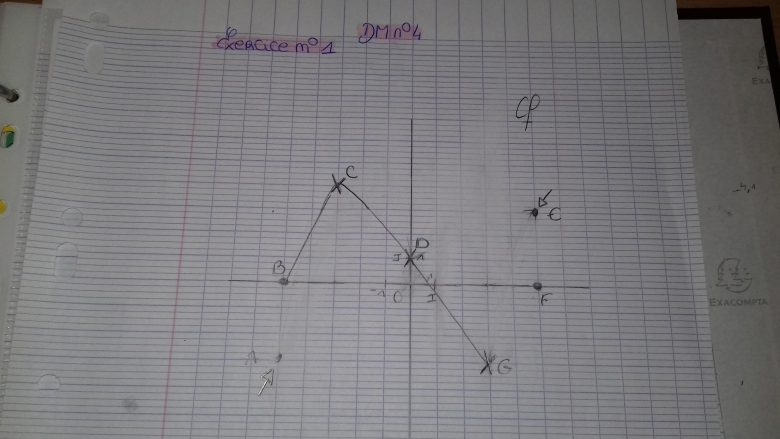
Vous remontez le point de départ au dessus de l'axe des abscisses
à droite tout ce qui est entre le point J et la flèche doit être changée
Vous joignez J et le point de coordonnées
On aura ainsi 2 points d'intersection de la courbe avec l'axe des abscisses
Un peu plus haut pour B puisqu'il ne faut que deux points sur l'axe des abscisses et vous reliez G à F
Il n'était pas nécessaire de redonner un nom à J, D est inutile.
Ne passez pas par F vous avez tracé un segment parallèle à l'axe des ordonnées. Ce n'est plus la représentation d'une fonction


 )
)