Inscription / Connexion Nouveau Sujet
représentation graphique de fonctions
Bonjour
soit la fonction de référence x ------> ex
et la fonction f telle que : x --------> f(x) = k.enx
ces deux fonctions étant tracées dans un plan rapporté à un repère orthonormé (O; ;
; )
)
Pouvez-vous m'expliquer comment on déduit la courbe représentative de f à partir de celle de la fonction de référence ?
Je pense qu'il s'agit d'une translation de vecteur  , mais je ne parviens pas à l'exprimer de façon générale, pour tout k et pour tout n.
, mais je ne parviens pas à l'exprimer de façon générale, pour tout k et pour tout n.
Merci d'avance
Bonjour,
une translation d'une courbe y = f(x) du vecteur  donne la courbe y = f(x) + 1
donne la courbe y = f(x) + 1
donc rien à voir.
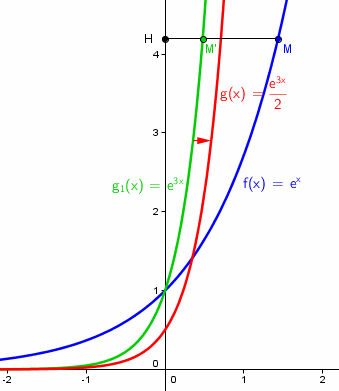
tu aurais vraiment l'impression que par exemple cette courbe g(x) est obtenue par translation de f(x) du vecteur  ????
????
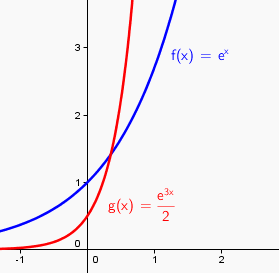
que veut dire, géométriquement, multiplier les coordonnées y par k ?
que veut dire, géométriquement, multiplier les coordonnées x par n ?
(que la courbe f(x) soit y = ex ou pas)
Bonjour,
Soit M (x ; ex)
M' (x ; ex)
M" (0 ; ex)
Calcule les coordonnées des vecteurs MM' et MM" et tu auras peut-être une idée
>> Mathafou + >> jeveuxbientaider
merci d'essayer de m'aider
>> Mathafou : c'est un bon exemple, mais je ne vois pas comment on passe par une formule générale de la courbe de f à celle de g. J'essaye de répondre à tes questions, mais j'ai du mal.
multiplier x par n, ou multiplier y par k, je comprends que ce sont les questions à se poser mais je n'arrive pas à le formuler pour en déduire des lois générales.
Peux-tu m'aider plu stp ?
>> jeveuxbientaider alors je ne comprends pas où ça doit aboutir...
multiplier x et ou y par une constante c'est un changement d'échelle
il n'y aura rien de plus à ce niveau
le fait que c'est une fonction exponentielle permet d'écrire toutefois
k.enx = enx + b (avec b = ln(k))
ce qui permet d'écrire ça sous la forme d'un changement d'échelle (multiplication par n : HM' = HM/3)
et (suivi) d'un décalage (translation) selon l'axe des x
(addition de b, translation de ln(2)/3, divisé par 3 à cause du changement d'échelle)