Bonjour
là tu écris des résultats mais on ne voit pas le raisonnement

1) OK pour la représentation paramétrique

ensuite, cherche l'intersection de cette droite avec le plan, d'où une valeur de t

enfin, calcule la distance demandée

Bonjour,
2) Tu devrais commencer par déterminer le point d'intersection de la droite  d  et du plan  P .

Bonjour à vous deux,
en recopiant je viens de me rendre compte que j'avais fait une erreur dans le début donc
1) x=1+2t
y=a                  t
z=a²-t

ensuite
1= 1 +2t               je trouve t= 0
a=a                                      t=0  
a²=a²+t                                t=0


je bloque j'ai fait
2*1+a-2a²-3=0
a-2a²=3
a-2a²=1

vous voyez je ne sais plus quoi faire.

MERCI

tu prends un point quelconque de ta droite
x=1+2t
y=a t
z=a²-t

et tu dis qu'il doit appartenir au plan d'équation 2x-z-3=0
soit
2(1+2t)-(a²-t)-3=0
cela va te donner la valeur de t (en fonction de a) correspondant au point de la droite, qui est sur le plan également

Re,

je ne vois vraiment pas
j'ai essayé en mettant 1 à la place de a
j'ai donc t=3/4  pour a=1

si je prend a=2 je trouve t=1

je ne vois pas comment faire

MERCI

tu dois tirer t de cette égalité
et ton résultat va s'écrire en fonction de a, cela veut dire que la lettre a va rester dans ton résultat
tu ne dois pas remplacer a par une valeur particulière

Bonjour  à vous 2,

vous êtes sûr de y=a t comme point de la droite?

ce n'est y=y_A+0 t ? puisque

MerciPirho
c'est moi qui ai fait une erreur de recopie en faisant un copier coller
> Nelcar
donc pour la droite, c'est
{x=1+2t
{y=a
{z=a²-t

et tu injectes cela dans ton équation de plan, pour trouver la valeur de t en fonction de la lettre a

Pirho, tu peux reprendre la main, si tu es libre ...?

de rien, ça arrive aux meilleures

Re,
oui j'avais vu mais là je n'avais pas eu le temps de répondre

donc ok pour
x=1+2t
y=a                  t
z=a²-t  
c'est ce que j'avais mis à 10 h 43

je vais donc
2(1+2t) -a - 3(a²-t) -3 = 0
2+4t-a-3a²+3t-3=
7t -a-3a²-1=0
7t=a-3a²+1

t=(a-3a²+1)/7

mais.....

MERCI

as-tu fait ce dessin, voir ce qui se passe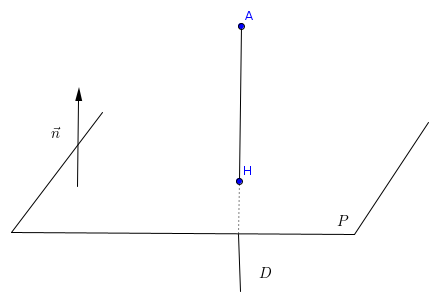


on projette donc A sur le plan P
et tu es en train de chercher l'intersection de la droite D avec P

ensuite tu pourras calculer la distance AH



vois-tu un peu mieux où tu vas ?

Re,

oui en effet j'ai omis et j'ai ajouté donc j'ai :

2(1+2t) -0* a - (a²-t) -3 = 0

là j'ai trouvé
t=(a²+1)/5

pour la suite j'ai du mal

MERCI

t : c'est juste.
Tu peux maintenant calculer les coordonnées du point d'intersection d-P.

on peut calculer les coordonnées de H, mais ce n'est pas complètement indispensable

quand on écrit
x=1+2t
y=a
z=a²-t

en réalité on a écrit

{x=x_A+2t
{y=y_A
{z=z_A-t

ce qui peut s'écrire aussi

{x-xA=2t      {xH-xA=2t
{y-yA =0       {yH-yA  =0      
{z-zA=-t      {zH-zA=-t        
         
                                                                       

Re,
donc ok pour t

j'ai essayé mais j'ai du mal
donc je remplace t par (a²+1)/5
x=1+2(a²+1)/5=2a²+7
y=a
z=a²-(a²+1)/5=4a²+1
les coordonnées du point H (2a²+7 ; a ; 4a²+1)

mais j'avoue que je suis perdue là

MERCI

messages croisés, nous avons posté simultanément
tu t'es trompée dans tes calculs, tu as perdu tes dénominateurs

essaie de comprendre ce que j'ai dit juste au dessus, cela fera moins de calculs

Re,
donc j'ai essayé dans la formule  
AH= 2*(a²+1)/5-(a²+1)²/5
j'ai trouvé (2a²-a^')/5

MERCI

si je reprends mes résultats de 16h40


non ?

Re

moi j'avais remplacé t par sa valeur

tu avais noté :

x=1+2t
y=a
z=a²-t

en réalité on a écrit

{x=xA+2t
{y=yA
{z=zA-t

ce qui peut s'écrire aussi

{x-xA=2t      {xH-xA=2t
{y-yA =0       {yH-yA  =0      
{z-zA=-t      {zH-zA=-t        
        
    comme tu avais mis AH(xh+xa)²+(yh-xa)²+(zh-za)²

moi j'ai AH=(2t)²-t²       toi tu as + t² (je sais que -t*-t=+t² donc je suppose que c'est ça

donc l'exercice s'arrête là ou il y a encore quelque chose à faire

MERCI                                                  

eh oui, (-t)²=+t²

non, tu dois écrire le résultat en fonction de a pour pouvoir répondre à la question 2

Re,

donc je trouve a²+1

MERCI

sans oublier la racine



oui, et quelle est donc la plus petite valeur possible de cette expression, obtenue pour a = ? ....

Pas de souci Pirho...c'est parce que je savais que j'allais m'absenter, mais Nelcar est patiente, elle sait qu'on revient toujours
Oui, quand on poste quasi simultané, on ne voit pas nécessairement si une autre réponse va s'intercaler ou pas.

Re,

tu sais sûr pour
AH = a²+1   car moi j'arrive à AH= a²+1  (la racine pour moi a été annulée avec le carré mais je me suis peut-être trompée )

après pour la plus petite valeur de a je dirai 1

MERCI

tu as raison ! mais par contre il y a un "divisé par 5 en déroute à mon avis"



donc AH =

et maintenant que tu vas avoir fini ton exercice, je te donne cette fiche, car dans certains programmes, ceci est une formule de cours
Calcul de distances dans l'espace

ah oui, tu auras encore à dire quand AH est minimale...pour a= ....d'où le point A (le plus proche du plan)

Re,

pourquoi mets tu AH²

voici ce que j'ai
AH = '(a²+1)²/5 +(a²+1)²/5
je supprime la racine et le carré j'ai donc
AH = (4a²+4)/5 + (a²+1)/5 = (5a²+5)/5 je mets 5 en facteur donc 5(a²+1)/5 donc a²+1

MERCI

rha...

faudrait peut-être pas oublier de mettre également ton dénominateur au carré

car , non ?

j'ai mis AH² pour ne pas avoir à écrire la racine carrée, mais je suis d'accord qu'on cherche AH et non AH²
et au dernier moment, j'écris AH, une fois le calcul fait sur AH²

toutes tes erreurs sont des bêtes erreurs de calculs sur les programmes antérieurs

Bonsoir,
je n'ai pas pu me connecter (problème avec ma messagerie)
oui bien sûr que (a/2b)² est égal à a²/b²

donc est-ce bon ce que j'avais mis à savoir :
AH = '(a²+1)²/5 +(a²+1)²/5
je supprime la racine et le carré j'ai donc
AH = (4a²+4)/5 + (a²+1)/5 = (5a²+5)/5 je mets 5 en facteur donc 5(a²+1)/5 donc a²+1

MERCI

Bonjour
je suis d'accord avec ce que tu me met mais pour moi
AH =a²+1

je reprends :
{x-xA=2t      {xH-xA=2t
{y-yA =0       {yH-yA  =0      
{z-zA=-t      {zH-zA=-t        
        
    comme tu avais mis AH(xh+xa)²+(yh-xa)²+(zh-za)²

moi j'ai AH=(2t)²-t² = 4t²+t²=5t²
AH = 5t
AH= 5(a²+1)/5
je supprime le 5 en haut et en bas et ça me donne AH =a²+1

tu me dis où je me trompe

MERCI

en l'absence de malou

ce qui suit est faux(déjà dit)!

Bonjour

là :

Citation :
moi j'ai AH=(2t)²-t² = 4t²+t²=5t²
AH = 5t

Re,
ok
donc en résumé le résultat est  quoi car là je mélange le tout

MERCI

il suffit de remplacer t par sa valeur dans l'expression donnée par  malou

bonsoir,
je n'ai pu venir sur le site avant, désolée
je remplace en effet t par sa valeur  
moi j'ai AH=(2t)²-t² = 4t²+t²=5t²
AH = 5(a²+1)/5
je supprime le 5
ce qui me donne AH=(a²+1)

j'arrive toujours  au même résultat donc j'abandonne

MERCI

Bonjour,

si on veut bien me donner la réponse

c'est AB=a²+1
et la plus petite valeur de a c'est 1

MERCI

Je t'ai donné la réponse à plusieurs reprises

malou @ 13-01-2021 à 09:31

Bonjour

car si alors puisque ici t est positif vu son expression

Bonjour

Tu sais Malou j'ai énormément de mal avec les vecteurs (tout ce qui est dans l'espace je galère et j'ai vraiment du mal à voir).
Il y a des choses qui passent sans problèmes et d'autre que je bloque.

MERCI encore de ta patience