Inscription / Connexion Nouveau Sujet
Représenter une fonction f
Bonjour,
Pourriez-vous m'aider svp pour cette exercice :
f est définie sur [-3;5].
f admet un minimum absolu en 1.
f est positive ou nul pour tous x > ou egal a 3 .
-2 a pour antécédents 0.
f décroit uniquement sur [-1;1].
Je comprends f est définie sur [-3;5] et -2 a pour antécédents 0 (ce qui veut dire que la courbe passe -2 en y pour x=0
Par contre je ne comprends pas le reste ou presque, je pense me tromper
Pourriez-vous m'aider svp
merci par avance
Hello,
Un minimum absolu signifie que le minimum de la fonction sur [-3,5] est en 1, donc que la fonction ne "descendra" pas plus bas.
Comprends tu le reste?
bonsoir
peux-tu préciser ce qui te bloque ?
on est d'accord que lorsqu'on dit que la fonction f décroit sur tel intervalle, on parle de sa ...?
quelle est la question posée ? est-ce "proposer un tracé de courbe ?"
l'énoncé que tu écris est-il complet ?
tu as complété un tableau de variation ?
Bonsoir Carita,
Merci de me répondre, en fait il faut faire la courbe sur un repère orthonormal au pas de 1
il n'y a pas de tableau de variation à faire, il faut juste tracer la courbe avec les informations ci-dessus.
Merci pour ton aide
j'entends bien que le tableau de variation n'est pas obligatoire,
mais ça t'aiderait bien d'essayer d'en compléter un avec les données que tu disposes.
dans l'absolu, il y a, avec ces seules données, une infinité de façons de tracer "la" courbe.
on te demande juste une tendance possible, telle que f remplisse ce cahier des charges.
tu n'as pas répondu à ma question :
" lorsqu'on dit que la fonction f décroit sur tel intervalle, on parle de sa ...?"
je pense que la courbe passe par -1 en abscisse et va jusqu'à -2 en ordonnée et remonte à 1 en abscisse ?
"courbe passe par -1 en abscisse "., " remonte à 1 en abscisse" .. pas très clair tout ça...
lorsqu'on dit que la fonction f décroit sur tel intervalle, on parle de sa variation.
"f décroit uniquement sur [-1;1]. " : signifie que pour -1  x
x 1, la fonction est décroissante,
1, la fonction est décroissante,
et seulement sur cet intervalle-là.
alors, quid de la variation possible sur les autres intervalles ?
---
si besoin de te convaincre d'ébaucher un tableau de variation :
tu as dû constater, quand tu as fait des études de fonctions,
que quand tu places les flèches, montantes ou descendantes, sur un tableau de variation,
ces flèches te donnent une idée de l'allure générale de la courbe, et c'est ça que l'on cherche pour proposer un tracé.
---
pour le tableau de variation, au brouillon :
sur la ligne des x, positionne les bornes de Df, ainsi que les autres valeurs de x pour lesquelles il se passe "quelque chose", selon l'énoncé.
puis prends les contraintes l'une après l'autre, réfléchis, et essaie de le compléter.
proposes-en un, je te dirai.
bonjour,
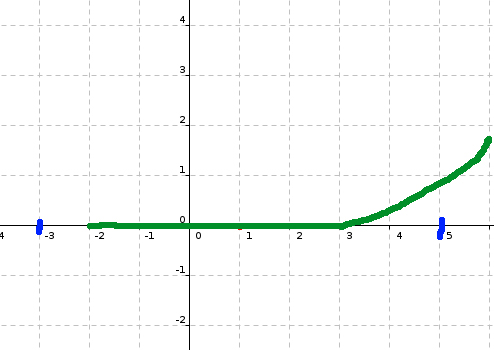
voilà la courbe que j'ai faite...
f admet un minimum en x=1 : le minimum est 0
f est positive ou nul pour x>=3 : ici la courbe monte
-2 a pour antécédent 0 donc f(-2)=0
f décroit uniquement sur [-1;1] : la courbe descend
encore une fois merci pour votre aide
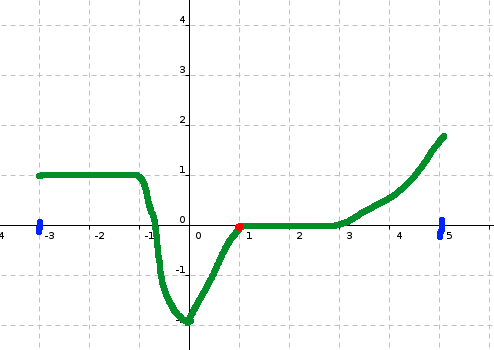
Ta courbe de 10h19 ne respecte pas deux conditions de l'énoncé : elle ne présente pas de minimum absolu en 1 et elle n'est pas décroissante de - 1 à 1 .
Ah oui zut je l'avais oublié
Comme ça peut etre, la deux conditions je ne vois pas et pour le tableau de variation c comme ma courbe, si la courbe est fausse, mon tableau aussi.
Bon je ne lâche pas lol
ligne de la dérivée :
ok entre -1 et 1 : la dérivée est négative puisque f décroit
ok aussi au-delà de 1 : pourquoi la dérivée est-elle forcément positive ?
en revanche, entre-3 et -1 la dérivée n'est pas obligatoirement positive : elle peut être nulle (f monotone sur l'intervalle)
là, on aura le choix pour la courbe.
dérivée nulle en 3? qu'est ce qui te fait penser ça ? sur quoi tu t'appuies ?
en fonction du signe de la dérivée, tu peux à présent placer tes flèches pour la variation.
ben en fait f est positive ou nul pour tous x>= 3 donc soit c'est 0 ou négatif, je crois avoir compris là
je ne suis pas sure de bien comprendre ta justification (?)
la fonction atteint son minimum absolu en 1;
et on sait (...) que ce minimum sera inférieur à -2 (qui est négatif)
puisque la fonction devient positive à partir de 3, il est obligatoire que la fonction soit croissante après 1.
d'accord ?
place tes flèches de variation
et propose une courbe
puisque la fonction devient positive à partir de 3, il est obligatoire que la fonction soit croissante après 1.
d'accord ? Là je ne comprends pas je pense, je dois mal placer ma courbe ? elle passe pourtant par 0 non ?
"-2 a pour antécédents 0. " --- tu en déduis que le point (...? ; ...?) appartient à Cf
ps : je rectifie une coquille de ma part
...en revanche, entre-3 et -1 la dérivée n'est pas obligatoirement positive : elle peut être nulle (f monotone constante sur l'intervalle)...
je laisse la main.
Ton ébauche de courbe de 10h19 est la meilleure de toutes. Essaie de l'améliorer (cf mon message de 12h08).
je suis coincé avec -2 a pour antécédents 0.
j'ai vu mon erreur avec (-1;1) mais je ne sais pas où faire passer le point -2 a pour antécédents 0.
Et j'avoue que là j'ai passé mon dimanche dessus et je commence à en avoir un peu marre lol
je craque 
Il ressemble à quoi en fait cette courbe, j'aimerai tout de même connaitre mon erreur
Sinon encore merci pour votre aide 
Mais tu as correctement fait passer la courbe par le point (O; 2), car si - 2 a pour antécédent 0 , on a f(0) = - 2 .
As-tu relu mon message de 12h08 où je te précisais ce qui n'allait pas dans ta courbe ?
oui pour le (-1;1), je ne comprends pas mon erreur sauf peut etre que mon dessin est mal fait. Où alors, décroit uniquement sur (-1;1) cela veut dire mais elle remontre où ? pfffff
ça ne veut rien dire
J'ai pigé je crois, le gros problème ne math c'est qu'il faut aussi comprendre le français, en fait décroit uniquement en (-1;1) cela veut que la courbe ne redescendra plus
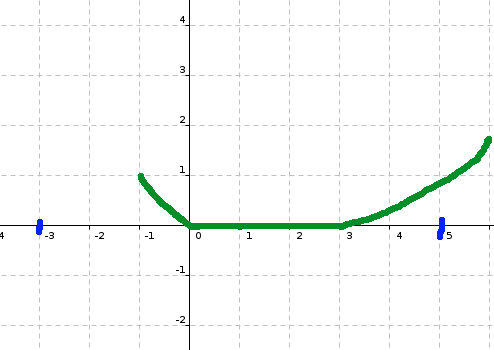
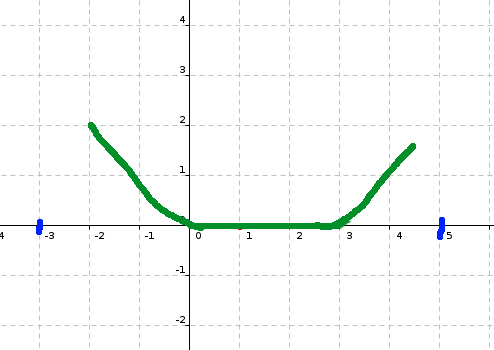
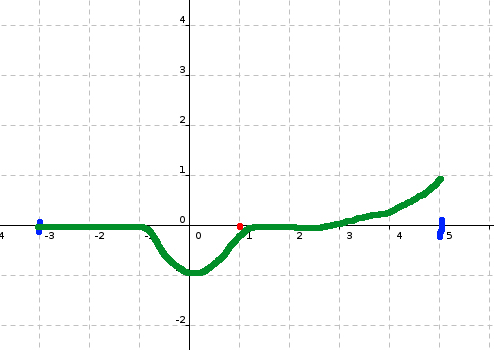
donc je propose ce graph
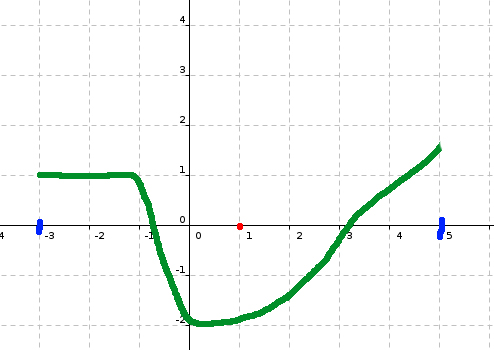
Maintenant, tu fais remonter la courbe dans l'intervalle [0; 1] et tu ne places en 1 pas le minimum absolu !
warback
lorsque tu as dessiné une courbe,
je te propose, courbe sous les yeux,
de relire chacune des contraintes de l'énoncé, et de contrôler si tu l'as respectée :
f est définie sur [-3;5].
f admet un minimum absolu en 1.
f est positive ou nul pour tous x > ou egal a 3 .
-2 a pour antécédents 0.
f décroit uniquement sur [-1;1].
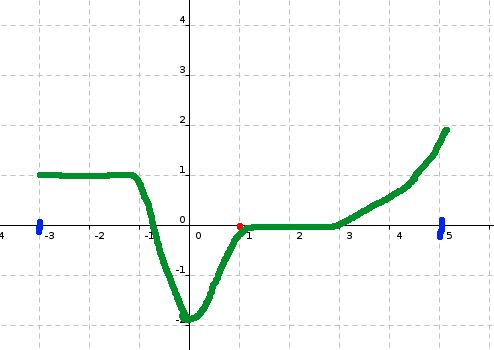
par exemple, sur les 2 derniers graphiques que tu as proposés,
il est évident que tu n'as pas respecté ceci : f décroit uniquement sur [-1;1] :
en effet, entre 0 et 1, tes courbes "remontent", alors que la fonction est décroissante.
coup de pouce :
personne n'a dit que -2 est le minimum global !
et ça tu l'aurais vu sur le tab. de variation... 

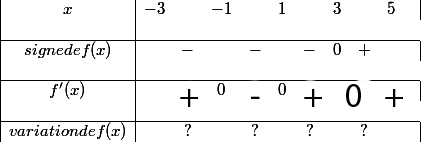

 analyse en Bts
analyse en Bts