Inscription / Connexion Nouveau Sujet
Résolution graphique
Bonjour,
je n'arrive pas à résoudre cet exercice:
On donne la représentation graphique de la fonction f définie par : x f(x)=x^3-x+5.
f(x)=x^3-x+5.
1.Construire la représentation graphique de la fonction g définie par : g(x)=x+5.
2.Résoudre graphiquement l'équation f(x)=g(x).
3.Résoudre graphiquement l'inéquation :
x^3-x+5 x+5.
x+5.
4.Résoudre algébriquement l'équation f(x)=g(x).
Merci d'avance.
j'ai fait un tableau pour trouver coordonnées de g(x): une fois x=0 donc(0;5) et x=2 donc (2;7). j'ai tracé la droite g(x)= x+5. après déduction si f(x) avec x=0 alors coordonnées (0;5). J'en déduis que f(x)=g(x). Là je n'avance plus. Pouvez-vous m'aider, merci.
bonjour,
1. c'est juste pour le tracé de la droite.
2. voici les deux courbes:
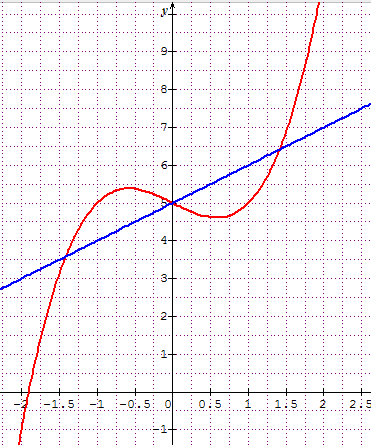
résoudre f(x0 = g(x) c'est trouver les abscisses des points d'intersections entre les deux courbes.
On les trouve en :
x = -1,4 ( environ)
x = 0
x = 1,4 ( environ)
3. resoudre graphiquement x^3-x+5\ge x+5, c'est trouver pour quels x la valeur f(x) sera plus grande que g(x) donc la courbe sera au dessus de la droite.
On cherche donc sur le graphique les abscisses des points qui verifient cela.
on obtient: [-1,4 ; 0] U [1,4 ; + [
[
4. <=>
<=>
<=>
<=>
les solutions sont donc



