Inscription / Connexion Nouveau Sujet
Résoudre graphiquement une inéquation
Bonjour,
Je dois rendre un DM de math mais je n'arrive pas à faire mon exercice, même après avoir consulté plusieurs cours sur les inéquations. L'exercice est le suivant:
Résolvez algébriquement et graphiquement les inéquations:
a) -2x+1/5 supérieur ou égal 0
b) 3/4x+1 supérieur 3
Merci d'avance
Bonsoir,
Pour la a), résolution algébrique :
-2x + 1/5 > 0
-2x > -1/5
2x < 1/5
x < 1/10
Pour la résolution graphique, il suffit de tracer la droite d'équation -2x + 1/5, et de regarder quand celle-ci est au-dessus de l'axe des abscisses.
On constante que retrouve bien les solutions qu'on avait trouvé algébriquement :
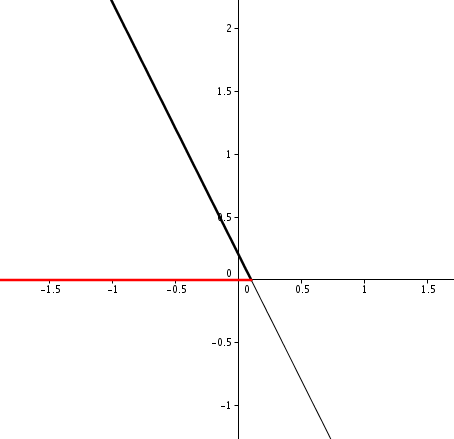
Pour la b), c'est le même principe que la a), en essayant de se ramener à quelque chose de la forme ... > 0.
En l'occurrence, 3/4x+1 > 3 est équivalent à 3/4x-2 > 0.
Bonsoir, et merci d'avoir répondu.
Pouvez-vous me dire comment l'on doit s'y prendre étape par étape pour résoudre graphiquement une inéquation? Car je suis très mauvaise en math et je ne sais pas du tout comment m'y prendre!
Il suffit de tracer la fonction qui se cache dans le membre de gauche de l'inéquation, et celle qui se cache dans le membre de droite.
Par exemple, dans l'équation a), on a deux fonctions :
— dans le membre de gauche, la fonction qui à x associe -2x+1/5 ;
— dans le membre de droite, la fonction qui à x associe 0 (autrement dit une fonction constante).
Les deux fonctions auront donc, dans ce cas, pour représentation graphique respectivement une droite de pente négative (la première fonction est une fonction affine) et une droite horizontale (en fait, ici, c'est l'axe des abscisses !).
Normalement jusqu'à ça ne devrait pas poser trop de problèmes, les fonctions affines/linéaires/constantes, c'est du programme de 3e. 
Ensuite, une fois les deux courbes tracées, il suffit de regarder quand l'une est plus au-dessus que l'autre.
Dans le cas de a), on cherche à avoir -2x+1/5 > 0, donc on regarde quand la droite en noire est au-dessus de l'axe des abscisses. On remarque (cf. dessin dans mon précédent message) que c'est le cas sur la partie tracée en gras. Les solutions sont alors les abscisses de ces points (autrement dit, tous les points en rouge sur le dessin précédent).


