Inscription / Connexion Nouveau Sujet
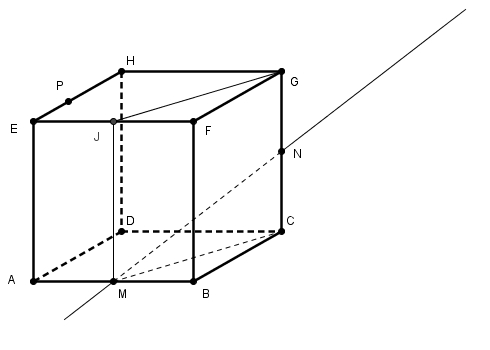
Pourquoi joindre N à H ? Ce n'est dans aucune face du cube.
Essaye d'utiliser le même point I que dans ton exercice.
là c'est en train de partir en quenouille en vertu de la règle : un sujet = un exercice
accentué par le passage à la page 2 de la discussion (figures plus visibles et textes plus visibles)
"joindre N à H" c'était à propos d'une variante (la variante difficile pour laquelle aucune paire de points donnés n'est sur une même face) et c'est effectivement de toute façon faux.
alors que "le même point I que dans ton exercice" c'est pour l'autre variante plus facile (M et N comme dans l'exercice et juste P libre sur la face (EFGH))
on ne va pas courir deux lièvres à la fois
OK pour la variante simple (en disant en texte que tu termines par des parallèles)
ou avec la construction "à la règle seule" comme Zormuche (sans besoin de parallèles)
on peut donc attaquer la variante ardue.
le problème est ici qu'aucune des seules droites que l'on sait être dans le plan (MNP), à savoir (MN) (NP) et (MP), n'est dans une des faces du cube
(alors que (MN) l'était dans les variantes simples)
l'idée de chercher l'intersection de (MN) avec le plan (EFG) en un certain point I est bonne.
car alors l'intersection de (MNP) et du plan (EFG) sera là aussi la droite (IP)
mais sa réalisation nécessite une étape intermédiaire :
par un autre plan que (MNP), mais qui contiendrait la droite (MN)
et dont l'intersection avec (EFG) serait "facile à tracer"
l'intersection de (MN) avec (EFG) serait alors l'intersection de (MN) avec cette intersection là.
(pour l'instant P n'a pas son mot à dire là dedans)
plusieurs plans auxiliaires peuvent être choisis à cet usage
je te propose un plan vertical passant par M et N ...
Pour [JG] et [MB] :
De manière générale, si la section contient un "morceau" d'arête, alors toute l'arête y est.
Tu as tendance à emprunter le chemin d'une arête quand te ne sais pas quoi faire.
Essaye de perdre cette habitude
je te propose un plan vertical passant par M et N ...
Plan vertical : qui contient une droite verticale, par exemple la droite verticale qui passe par N .
pour l'instant la seule chose qu'on sait du plan (MNP) est les points M,N,P et les droites (MN), (MP) et (NP)
aucun autre point de ce plan n'est connu
le seul moyen d'obtenir d'autres éléments (pour pouvoir tracer des droites de ce plan qui seraient aussi sur les faces du cube) est d'utiliser ces droites là
donc de commencer par construire le point d'intersection précis de la droite (MN) avec le plan (EFG)
RIEN d'autre n'est disponible tant que ce point là ne sera pas construit
toutes tes tentatives de sections sans utiliser ce point que pour l'instant on cherche ne représentent absolument rien du tout
(sont fausses et archi fausses)
quant au théorème du toit il va servir ici juste pour cette sorte d'évidence de tracer la section du cube par un plan vertical (c'est à dire parallèle à l'arête (BF))
et on sait faire ça (tracer la section d'un pavé par un plan vertical) depuis la 5ème !
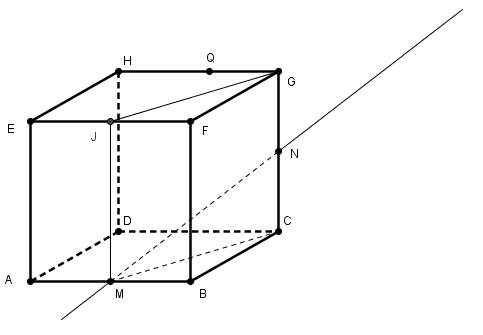
est-il vraiment indispensable d'invoquer le théorème du toit pour justifier que MJ est parallèle à BF ??
le plan vertical dont je parle est le plan MCGJ
et on ne perd pas l'objectif de cette construction annexe : trouver le point d'intersection de la droite (MN) avec (EFGH)
donc continuer cette construction du point I, intersection de (MN) et (EFG)
(indice : utiliser bien entendu le plan (MCGJ) pour ça , c'est à ça qu'il sert !)
puis utiliser ce point I pour construire le morceau de section sur la face (EFGH) du cube par le plan (MNP)
en effet I appartient à (MN) donc à (MNP) et aussi à (EFG) par construction,
donc à l'intersection cherchée de (MNP) et de (EFG)