Inscription / Connexion Nouveau Sujet
Section dans Géométrie dans l'espace
Bonjour à tous,
Je fini mes révisions pour le bac mais malheureusement je n'arrive toujours pas à faire des section dans la géométrie dans l'espace... J'ai beau essayer et essayer mais rien ne viens.. C'est un problème de méthode je pense.
Par exemple dans cet exercice:
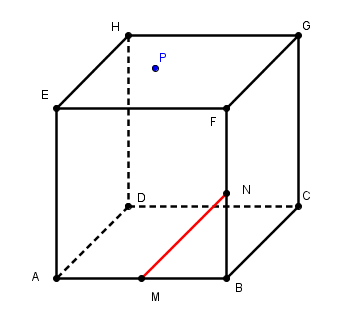
Soit ABCDEFGH un cube. M et N sont les milieux respectifs des arêtes [AB] et [BF]. P est un point appartenant au segment [GH].
On se propose de construire la section du cube par le plan (MNP).
Je suis certaine que c'est tout simple mais pour moi cela semble quasiment impossible, ce que je fais ne ressemble pas du tout à une section.
Est-ce que quelqu'un pourrait m'aider s'il vous plaît?
Merci beaucoup !! 
Certains éléments de la section cherchée sont connus : le point P et le segment [MN].
Ce segment est l'intersection du plan (MNP) et du plan de la face ABFE.
Peux-tu déterminer alors l'intersection du plan (MNP) et du plan de la face DCGH ?
Bonjour,
peut être que si tu donnais ta (tentative de) solution, on pourrait te dire si c'est juste ou faux et te corriger / compléter ?
parce que il y a ses tas de façons de faire cette construction, alors autant prendre celle d'où tu es parti ...
pour joindre une figure : lire la FAQ.
Bonjour,
Ce n'est pas tout simple !
La difficulté est de démarrer.
Le point P est à l'intersection de deux faces du cube. Il faut commencer par travailler dans ces deux faces, en utilisant leur lien avec la face ABFE qui contient le segment [MN].
L'une de ces faces est parallèle à la face ABFE .
On peut donc y tracer la parallèle à (MN) issue de P .
L'autre face où se trouve P a une arête commune avec ABFE . La prolonger pour construire l'intersection avec (MN) de cette arête.
Donne des noms aux points que tu utilises.
Bonjour mathafou 
Je te laisse continuer, tu es plus pédagogue que moi dans ce domaine.
Et tu fais facilement de superbes figures !
Salut,
Par ailleurs, quand un texte d'exo commence par :
"On se propose de construire la section du cube par le plan (MNP). "
Ca veut en général dire : "on va le faire à l'aide des questions qui suivent" (sinon, il y aurait écrit : "Construire la section du cube par le plan (MNP)."
Donc :
Il n'y a pas des questions intermédiaires ensuite ?
Du genre : " les droites machin et truc se coupent en K, construire K, etc..."
j'avais aussi répondu sans avoir lu la réponse de Priam,
on va surtout laisser dirtsasioner digérer tout ça...
Bonjour,
J'ai trouvé ceci mais sans méthode particulière c'est pour cela que je me demande si c'est bon ou non...
J'ai commencé par tracer MN puis j'ai tracé une parallèle à MN en passant par P et le reste je l'ai fait par hasard...
Désolée d'être si peu précise je suis un peu perdue...
PS: ne prenez pas en compte les traits en pointillés, c'était des essais 
***image tournée, tiens ton téléphone dans l'autre sens...***
au hasard ??? en mathématiques ???
MN et parallèle à MN passant par P : OK
le reste c'est comme le dit Priam : chercher l'intersection de la droite (MN) avec le plan (EFGH) et en déduire l'intersection de (MNP) avec le plan (EFGH)
Le coup du "tracer des parallèles situées sur des faces parallèles" marche très bien (et ce n'est donc pas du tracé au pif, c'est un théorème).
ceci étant, tu peux en général t'en sortir en prolongeant judicieusement certaines droites, puis joindre leur intersection avec des points connus.
Ici par exemple, prolonge (MN) et (EF) , puis joints leur intersection avec P...
Cette construction fournit un point (le point I) de l'intersection des plans (MNP) et (EFG), dont un autre point est déjà connu.
Nota :
sur cette vue la parallèle en P est sur la face CDHG elle devrait donc être en pointillés (face cachée)
par contre je ne vois pas pourquoi les droites qui se coupent en I le seraient : elles sont sur des faces visibles
le non respect des conventions sur les parties cachées ou pas rend la "lecture" d'une telle figure difficile, perdant la notion de relief induite par ces conventions.
Je réponds pour la parallèle à (MN) issue de P que tu as tracée :
Elle est correcte ; je répète que ce n'est pas du tracé au pif ; mais elle serait mieux en pointillé car elle est "derrière".
L'autre face où se trouve P a une arête commune avec ABFE . La prolonger pour construire l'intersection avec (MN) de cette arête.
Et aussi de Priam :
Cette construction fournit un point (le point I) de l'intersection des plans (MNP) et (EFG), dont un autre point est déjà connu.
Bref, les points P et I se trouve dans le plan de la face EFGH .
Priam t'a répondu à 11:31 : obtenir un point de l'intersection du plan (MNP) avec la face supérieure (EFG)
et Yzz t'avait même dit à 11:01 exactement quoi en faire de ce point ...
ensuite tu as déja suffisamment d'intersections, sur les plans (ABE) (EFG) et même (BCF) et (CDG), pour terminer par le même coup des parallèles que tu avais utilisé pour la face arrière (CDG).
Ok! Donc ça donnerait ceci?
Auriez-vous un autre exercice pour voir si j'ai compris?
Merci mille fois!
Par contre j'ai compris comment on faisait le point I mais toujours pas à quoi il sert... 
Est-ce qu'il sert juste à justifier que P et I sont dans le même plan ou bien il a une autre utilité?
le point I mais toujours pas à quoi il sert...
l'intersection du plan (MNP) et du plan (EFG) est une droite
qui contient le point P (trivial, énoncé) et le point I :
car ce point I appartient à la droite (MN) qui fait partie de (MNP) et à la droite (EF) qui fait partie de (EFG)
donc ce point appartient aux deux plans, donc à leur intersection qui est je rappelle ce qu'on cherche.
(intersections de (MNP) avec chacune des faces du cube)
et c'est pour ça qu'on l'a cherché et construit ce point I
pour avoir un point de cette fameuse intersection de (MNP) avec (EFG) (déja dit)
... prolonge (MN) et (EF) , puis joints leur intersection [c'est le point I] avec P...
tu as une drôle de façon de joindre le point I et le point P, toi ...
et c'est ça qui va te donner la partie de section avec la face (EFGH)
et ensuite avec la face (BCGF)
si ça n'est pas bon au départ tout le reste et du pipi de chat.
non dirtsasioner mais tu y es presque
trace le segment [IP]
Puis note l'intersection de [IP] et [GF] comme tu veux car elle est importante
ce qui est bien avec le point I c'est qu'il appartient au plan (puisqu'il appartient à (MN))
Et en plus il appartient à la face du haut du cube
Il ne reste plus qu'à le relier avec un autre point du plan en question (Le point P, par exemple) pour obtenir une droite IP qui appartient au plan (MNP) et à la face du haut
ca doit ressembler à ça :
comprends-tu mieux ?
L'intérêt est de trouver sur chaque arête un point appartenant au plan (sur chaque arrête que le plan croise)
On se retrouve avec un grand triangle IJK qui appartient au plan (MNP) et qui permet de placer les points intermédiaires sur chaque arête
mais tu y es presque
Je pense avoir compris!! 
Je vous montre ce que j'ai fait étape par étape:
Tout d'abord j'ai tracé [MN].
Ensuite j'ai prolongé (MN) et j'ai coupé cette droite avec la droite (EF) qui a donc donné I.
Puis j'ai tracé (PI).
Puis j'ai tracé la parallèle de MN j=en passant par P, ensuite la parallèle de (JN) (désolée j'avais oublié de mettre un nom au point d'intersection de la droite (FG) et (PI)).
Et pour finir j'ai relié les deux dernier points entre eux!
Je crois que j'y suis !! Merci à tous !
Auriez-vous un autre exercice à faire par hasard, du même type...?
c'est une façon de faire (en plus à la règle seule !)
remarque : Geogebra 3D rend des figures illisibles car bien trop "peintes" on ne peut même pas lire les noms des points !!
donc description verbeuse sur ces noms de points absents car illisibles
"le segment sur la face arrière" était tracé dans cette discussion par une parallèle :
l'intersection de deux plans parallèles par un même plan est deux droites parallèles
les constructions via J et K sont donc une autre méthode que celle commencée ici.
parce que il y a ses tas de façons de faire cette construction, alors autant prendre celle d'où tu es parti ...
Auriez-vous un autre exercice à faire par hasard, du même type...?
ce n'est pas ce qui manque !! il y en a plein dans l'ile si tu demandes à un moteur de recherche "construire la section"
plus compliqué : tu peux prendre M milieu de AB, N milieu de CG et P un point (quelconque) de EH

à mon avis ça va t'occuper un bon bout de temps pour identifier les plans et droites qu'il faut utiliser pour construire leurs intersections.
sans aller jusque là tu peux reprendre les données de l'énoncé (M milieu de AB et N milieu de BF) en libérant un peu plus P :
P un point quelconque de la face (EFGH)
la constriction est un peu semblable, à quelques détails près...
J'ai mis un peu trop d'opacité sur geogebra 
dirtsasioner pour l'intersection de [AD] et (MNP) ce n'est pas encore ça
Il faut procéder de la même façon que tu as trouvé le point I
Prolonge le segment sur la face arrière jusqu'à ce qu'il croise la droite (DC)
Merci Zormuche et mathafou ! J'ai corrigé sur ma copie !
Je vais maintenant tester votre exercice mathafou !
Zormuche
non.
c'est exactement ça.
(intersections de plans parallèles par un même plan = droites parallèles
on peut donc parfaitement tracer les 3 dernières intersections manquantes avec juste des parallèles
comme je le soulignais ta construction via tes points J et K est une autre façon de faire
qui a l'avantage de n'utiliser que de simples droites ("la règle seule") et est donc identique si le solide ABCDEFGH n'est pas un cube du tout mais un hexaedre (6 faces planes) quelconque.
tiens petit exo rigolo : construire une vue en perspective correcte d'un hexaèdre quelconque ayant effectivement toutes ses faces planes
(et pas des quadrilatères "gauches" = vrillés dans l'espace)
là aussi on est amené à considérer des intersection d'arêtes d'une même face pour construire les intersections de plans de l'hexaèdre...
et que ce soit des droites ...
Commence avec
sans aller jusque là tu peux reprendre les données de l'énoncé (M milieu de AB et N milieu de BF) en libérant un peu plus P :
P un point quelconque de la face (EFGH)
Comme te le conseille mathafou. C'est moins difficile

Dans ta figure (PJ) et (MB) ne sont pas parallèles alors qu'ils sont dans deux faces parallèles du cube.
De manière générale, si la section contient un "morceau" d'arête, alors toute l'arête y est.
Tu as tendance à emprunter le chemin d'une arête quand te ne sais pas quoi faire.
Essaye de perdre cette habitude
faux
MB ne fait évidemment pas partie de la section (il serait en vertu de la propriété rappelée plusieurs fois ici parallèle à JP ??)
section que tu as d'ailleurs tracée là aussi totalement au pif sans aucune construction véritable
les points I, J et K (sur BC) doivent être construits de façon rigoureuse et certainement pas choisis au hasard à vue de nez.
les traits et points auxiliaires de construction doivent figurer sur la copie
et le protocole de construction détaillé.
Mais avant de te lancer dans cet exo réellement difficile cherche juste déja la variante plus simple :
sans aller jusque là tu peux reprendre les données de l'énoncé (M milieu de AB et N milieu de BF) en libérant un peu plus P :
P un point quelconque de la face (EFGH)
fais déja ça (réellement)
ça permettra de vérifier que tu as compris ces histoires d'intersections via des pointa auxiliaires (le point I du premier exo)
Excusez-moi mais j'essaie de faire l'exercice mais je n'y arrive vraiment pas... Je commence par tracer pleins de traits de constructions mais ça ne donne rien de bon.
Si je commence par relier N à H que puis-je faire par la suite?




