Inscription / Connexion Nouveau Sujet
séparation des variables et théroèmes de Fubini-Tonelli
Bonjour,
Je ne comprends pas bien dans quels cas on peut séparer les variables lors que l'application de Fubini-Tonelli:
On est arrivé à transformer une intégrale double en deux intégrales simples emboîtées (selon Fubini ou Tonelli peu importe ici). Ensuite on réalise que l'intégrande f peut s'écrire f(x)=f1(x1) x f2(x2) pr tt x=(x1,x2) du domaine à intégrer.
Peut-on directement séparer les intégrales pour écrire leur produit où faut-il vérifier que le domaine est aussi "séparable", ie qu'il est cartésien en coordonnées cartésiennes ou "part d'un disque" en coordonnées polaire ?
salut
pour tout théorème il y a :
1/ des hypothèses
2/ une conclusion (lorsque ces hypothèses sont vérifiées)
alors donne :
a/ le théorème complet
b/ un exemple concret
Voilà le théorème (en vert) et la partie traitant des cas "variables séparables" (en bleu).
Prenons l'exemple de la fonction f(x,y)=xy définie sur .
On est sur donc l'espace produit est bien
-fini. On le muni de la mesure produit de Lebesgue.
On cherche à intégrer cette fonction sur le domaine D suivant:
0
x1
0y1-x
Cette fonction est (continue donc) mesurable et positive sur D.
On applique donc le théorème de Tonelli: ((mesures non notées correctement...))
En effectuant ce calcul je trouve 1/24, je sais pas si c'est juste mais ça tient la route (réel positif inférieur à 1).
Si maintenant j'applique la remarque bleue je trouve , ce qui n'a pas de sens. Et dans cet exemple le domaine d'intégration n'est clairement pas cartésien.
Dans cette remarque (bleue) manque-t-il une hypothèse sur les domaines ou est-elle inclue quand on parle de fonction produit? ((comme pour les couples de variables aléatoires où pour les mêmes raisons on demande à l'espace produit des supports d'être cartésien)).
ben non tu ne peux pas appliquer la remarque 2 comme tu le fais puisque les bornes d'intégration suivant la variable y dépendent de la variable x
cela marche par exemple pour le domaine 0 < x < 1 et 0 < y < 1
à vérifier ...
Oui les bornes dépendent de x, mais qu'est ce qui dit dans la remarque 2 que les bornes ne doivent pas dépendre de x ? (Je ne le vois pas clairement en la lisant et je n'ai jamais compris le théorème de Fubini pensant qu'il parlait de séparation des variables alors que pas du tt ...).
Merci pour le document (que j'ai déjà lu 
mais il parle de Fubini et d'interversion pas de séparation des variables).
il parle de Fubini et d'interversion pas de séparation des variables).
effectivement; personnellement je pense qu'on peut séparer les variables à condition de bien fixer les bornes et sous réserve que les fonctions soient intégrables
si GBZM passe par ici, il nous donnera sûrement un avis rigoureux et éclairé, comme d'habitude
jbsph
Voici un exemple calculé de 2 manières différentes
PDF - 72 Ko
conclusion :
En effectuant ce calcul je trouve 1/24, je sais pas si c'est juste mais ça tient la route (réel positif inférieur à 1).
Si maintenant j'applique la remarque bleue je trouve
Le voilà.
je suis d'accord qu'il s'agit ici d'intégrales emboîtées et qu'on ne peut pas séparer. Mais la fonction est pourtant un produit, alors d'après la remarque bleue on devrait pouvoir séparer?!
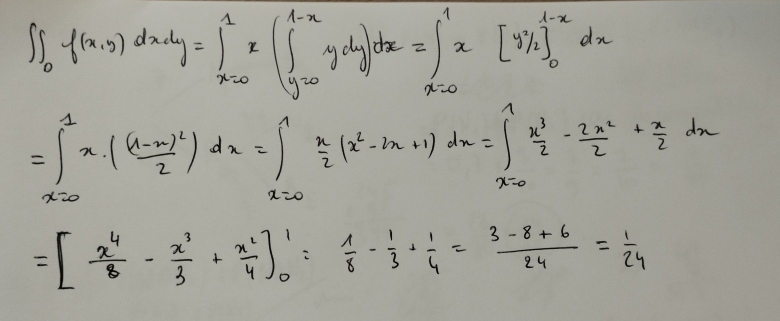
Bonjour,
Dans le texte il est indiqué "l'espace produit X = X1 × X2 ... pour tout pavé (ou rectangle)", ne serait pas cela qui indique "que les bornes y ne doivent pas dépendre de x".
(Je suis physicien, j'ai peut-être du mal à traduire...)
non Pirho : toujours à jbsph
parce que c'est aussi là que je voulais arriver pour montrer ce jeu de permutation avec les bornes !!
parce qu'il est que que
Si maintenant j'applique la remarque bleue je trouve
Dans ce cas on peut inverser l'ordre d'intégration? Mais ce n'est pas "un scoop", la fonction étant positive et mesurable ce résultat est assuré par Tonelli.
Dans ce cas on peut inverser, ok. Mais est-ce le domaine d'intégration qui empêche de séparer les variables ?
comme la dit gts2 à 20h49 : c'est le problème des bornes qui ne sont pas indépendantes des variables.
on peut donc intégrer dans l'ordre que l'ont veut mais il faut adapter les bornes aux variables d'intégration et dans le cas présent 0 < x + y < 1 donne 0 < x < 1 - y si on commence par x et donne 0 < y < 1 - x si on commence par y : pour chaque variable les bornes dépendent de l'autre variable pour la première intégration
D'accord. L'adaptation des bornes au sens d'intégration nous empêche de séparer les intégrales. Donc pour pouvoir séparer les variables il faut vérifier deux choses: un domaine "séparable" ie que le domaine soit le produit des projections sur chaque axe et que l'intégrande soit un produit ?
le domaine soit le produit des projections sur chaque axe
Pour moi c'est ce que signifie :
"l'espace produit X = X1 × X2 ... pour tout pavé (ou rectangle)"
Mais je ne suis pas mathématicien, donc si quelqu'un pouvait confirmer.
D'accord. L'adaptation des bornes au sens d'intégration nous empêche de séparer les intégrales. Non : on peut et c'est ce qu'on fait d'ailleurs quasiment toujours dans quasiment toutes les intégrales "élémentaires" : une double intégrale est la "succession de deux intégrations (justifiées par les théorèmes afférents)
parfois l'ordre s'impose naturellement mais on peut presque toujours la faire dans n'importe quel ordre, en adaptant les bornes ...
Donc pour pouvoir séparer les variables il faut vérifier deux choses: un domaine "séparable" ie que le domaine soit le produit des projections sur chaque axe et que l'intégrande soit un produit ? oui et non comme le montre l'exemple de Pirho ... et ce qui a été dit au-dessus
on sépare donc toujours les variables ... en adaptant le domaine d'intégration quand c'est nécessaire et il n'y a rien à adapter pour un pavé.
OK, mais je crois qu'on utilise pas le même vocabulaire, intégrales emboîtées (ou successives) signifie:
et intégrales séparées signifie: , où
Dans ce cas, Fubini ou Tonelli permettent de calculer une intégrale multiple en effectuant le calcul des intégrales successives. (mais pas de faire des intégrales séparées ?)
Dans les exemples au dessus les intégrales sont successives et non séparées?!
Mon questionnement portait sur comment passer d'intégrales successives à des intégrales séparées. (que la fonction s'écrive comme un produit ne suffit pas d'après ce qui est dit plus haut).
Annuler
connectez vous
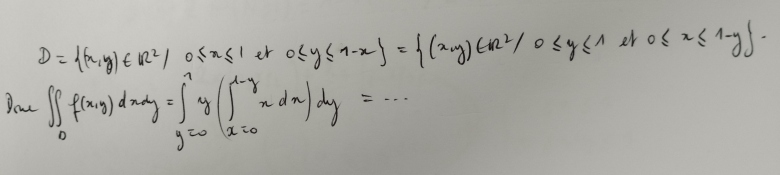
analyse en post-bac