Inscription / Connexion Nouveau Sujet
Séries de Fourier -Coeffcients et fonctions à partir d'un graphe
Bonjour à tous !
Je viens de commencer mon apprentissage des séries de Fourier dans le cadre de l'électronique. J'ai des exos à faire mais je ne vois pas comment les résoudre .... j'ai une idée globale de ce qu'il faut faire mais je n'arrive pas à commencer et je reste bloqué même en cherchant des indices sur le net.
Je dois déterminer la fonction à partir d'un graphe (l'image sera fournie) ainsi que les coefs a0 a1 et b1.
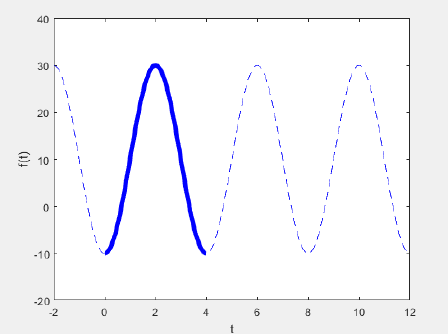
Déjà pour la fonction, je vois qu'elle est paire, la période est de 4 et l'amplitude de 40. Je sais que les séries de Fourier s'écrivent de la somme :
f(t) = a0/2 +  (an * cos((2
(an * cos((2 nt)/T) +
nt)/T) +  (bn * sin((2
(bn * sin((2 nt)/T)
nt)/T)
Comme cette fonction est paire, je sais déjà que la composante en sinus sera nulle donc je n'aurai que :
f(t) = a0/2 +  (an * cos((2
(an * cos((2 nt)/T)
nt)/T)
(donc je suppose que b1 vaudra 0 du coup)
Mais là où je bloque c'est comment trouver exactement la fonction f(t), j'ai bcp de données mais je n'arrive vraiment pas à trouver le lien logique pour que cet exercice découle tout seul et qui ne m'a pas l'air très dur.
Si quelqu'un pourrait m'aider, j'apprécierai. :'D
Merci d'avance.
bonjour : )
Tu as là un signal sinusoïdal, donc clairement, pour tout ,
avec
et
des réels à déterminer.
Tu as bien trouvé la période fondamentale, ce qui te donne . Tu as également déterminé la valeur crête à crête ce qui te donne
.
Pour finir, est donné par la valeur d'offset et
te donne
.
bonjour : )
Tu as là un signal sinusoïdal, donc clairement, pour tout
Tu as bien trouvé la période fondamentale, ce qui te donne
Pour finir,
Donc si j'ai bien compris :
a = 2
 n/T = 4 donc n
n/T = 4 donc n /2T et
/2T et
a1 = 40 et
 = - 10 ?
= - 10 ?
Et comment tu détermines la valeur d'offset de manière propre ? (qui a l'air d'être 2 ici)
Ton calcul de est étrange.
d'où
.
L'amplitude est également étrange,
(égale à la moitié de la valeur crête à crête dans notre cas de sinusoïde).
Bon, tu aurais du commencer par déterminer la valeur d'offset, elle a pour effet de translater ta courbe verticalement. C'est la composante continue de ton signal (on parle de valeur moyenne également) et tu lis clairement sur ton graphique que la sinusoïde est centrée en , donc
puis
.
Pour finir, , souviens toi de la courbe de la fonction cosinus et observe l'opposition de phase avec ton cas.
Note que les oscilloscopes sont capable de te donner chacun de ces éléments.
En bleu correspond ton signal original et en rouge l'offset est soustrait.
Utilise un outil graphique pour comprendre les effets des différents paramètres qui caractérisent un signal sinusoïdal. En tant qu'électronicien, tu as tout à gagné à savoir lire rapidement de tels signaux.
Pour revenir aux séries de Fourier en fait tu prendras garde à plutôt poser . Exepté
, tous les autres coefficients sont évidemment nuls.
Je m'en étais écarté un moment pour te faire prendre conscience de ton cas particulier.
Je ne suis pas un électronicien, je débute juste mais je comprends que tu veux dire et je souhaite vraiment que ce point noir devienne une chose aisée qui coule de source. :')
Je viens d'utiliser géogébra en regardant pas à pas les différents paramètres et en effet c'est bien cela.
Si jamais je dois mettre que c'est en opposition de phase juste à partir du graphique, tu crois que c'est possible de le démontrer de façon propre ? (quelque chose de plus rigoureux que "je vois et je sais que c'est ça")
Et oui je m'étais trompé pour l'amplitude parce que généralement quand je pense à l'amplitude c'est celle de crête à crête (comme sur les oscilloscopes) et pas juste l'amplitude entre le " 0 " et une crête.
Par ailleurs, même si je demande beaucoup, tu aurais un site qui détaille vraiment bien les séries de Fourier ? Je commence les transformées de Fourier, c'est assez simple à comprendre quand le prof explique mais je trouve pas ça ni évident ni naturel quand je dois résoudre un problème de ce sujet. :'(
En tout cas je te remercie pour ses réponses !
Par exemple, si j'écris :
10 + 20 cos(( /2)t +
/2)t +  ) = 30 ?
) = 30 ?
=>cos(( /2)t +
/2)t +  ) = 1
) = 1
Ce qui veut dire que :
( /2)t +
/2)t +  = 2
= 2
soit  = 2
= 2 -(
-(  /2) t =
/2) t =  (3/2)t donc :
(3/2)t donc :
 =
= *3 =
*3 = 
Penses tu que c'est logiquement bon et rigoureux ?
Ce n'est pas rigoureux. Mais je vois ce que tu souhaitais faire.
Pour déterminer analytiquement, je t'avais en fait demandé de regarder
.
d'où
puis
est UNE solution convenable.
Tu aurais pu regarder également,
etc. Ce que tu essayais de faire.
Je répondrai à tes autres questions demain.
Oui en effet j'ai fait le raisonnement à partir de f(2) qui revient à la même chose que f(0) :')
Je pense que je n'aurai pas d'autres questions, du moins, pas sur cet exercice donc on se reverra peut être sur un autre sujet. :')
En tout cas je te remercie beaucoup pour ton aide !
En fait, j'ai une dern ière question.
Je voudrais retrouver a0 et a1 avec les formules suivantes :
a0 = (2/T)  f(t) dt (avec les bornes de l'intégrale : 0 (borne inf)et T (borne sup)
f(t) dt (avec les bornes de l'intégrale : 0 (borne inf)et T (borne sup)
et
an = (2/T)  f(t)* cos((2
f(t)* cos((2 nt)/T) dt
nt)/T) dt
Quand j'essaie d'intégrer, je trouve toujours 0 (et même si la formule me dit T, je sais qu'il faut intégrer à T/2 pour trouver les bonnes valeurs)
Parce que l'intégrale de la fonction trouvée, je trouve : (40/ ) * sin(((
) * sin((( t)/2)+
t)/2)+ )
)
Tu aurais une idée de mon erreur ?
Je te rappelle que est périodique de période
. Donc son intégrale prise sur n'importe quel intervalle de longueur
est la même.
L'on a, pour tout ,
.
J'espère que tu trouves ce calcul évident. et
car
est
-périodique (tu peux faire le calcul par recherche de primitives si tu n'es pas convaincu, une primitive étant
).
Pour tout entier ,
par parité ;
et, en se souvenant que pour tous ,
, l'on obtient
Dernière ligne, lire :
Tu dois maintenant mieux réaliser qu'on pouvait se passer de ces calculs d'intégrales.
Aaaah mais je suis bête j'ai oublié l'intégrale de 10dt c'est pour ça que je trouvais toujours 0
Par contre j'ai l'impression de ne pas avoir compris ta dernière ligne, tu trouves une différence entre 3 cosinus alors que le produit de deux cosinus donne une addition de deux cosinus
Tu ne comprends pas la dernière ligne parce que tu oublies à nouveau que :
L'on a, pour tout
Tu ne comprends pas la dernière ligne parce que tu oublies à nouveau que :
L'on a, pour tout
Ah ben oui encore une fois ... Merci bcp du détail surtout pour m'avoir fait rappeler que les valeurs de l'intégrale identiques sur n'importe quel intervalle de la période fondamentale !
J'ai réessayé les calculs pour m'exercer mais je trouve (1-n) au lieu de (n-1)
Avoir un signe - de différence ça peut fausser les résultats des autres coefficients ?


 analyse en post-bac
analyse en post-bac