Annuler
connectez vous
arithmétique en post-bac
- Arithmétique dans Z - supérieur
- Exercice : le petit théorème de Fermat
- Ensemble et application Partie II
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Ensemble et application Partie I
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Licence Maths 1e ann ArithmétiqueTopics traitant de arithmétique [tout]Lister tous les topics de mathématiques
Niveau Licence Maths 1e ann
Sous groupe de Z/5Z et Z/6Z
Posté par Joaninha
Bonjour à tous,
Notre prof d'arithmétique nous a laissé en exo l'énoncé suivant :
Determiner les sous groupes de (
/5 , + ) et ceux de (/6, + )
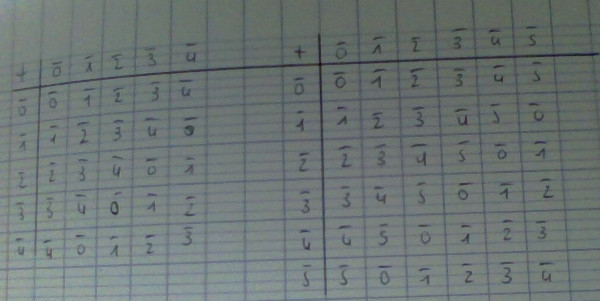
Idée : faire les tables et regarder les parties stables.
Ils nous a également donné les réponses. Mais je ne vois absolument pas ce que ça veut dire. J'ai donc fait mes tables.
Mais là encore je suis face à ça sans trop savoir ce qui m'indique un sous groupe. J'ai pourtant mes définitions dans la tête, mais visiblement concrètement c'est pas clair. Je ne comprends pas trop le "regarder les parties stables"
Enfin si quelqu'un pouvait m'aiguiller un peu ... merci 
Tout sous-groupe de est engendré par un de ses éléments.
Avec n=6, vois le sous-groupe engendré par .
On voit que leur inverse est eux même ... mais je suis désolée, c'est toujours pas évident...
Mon prof nous a donné comme réponse pour les sous groupes de /6 : 0, 2 et 4
ce n'est pas ça du coup ?
Il y a qui est un sous-groupe d'ordre 2 et
qui est un sous-groupe d'ordre 3... Sont-ce les seuls ? Pourquoi ?
Je suis désolée, je ne comprends toujours pas.
Je ne vois même pas ce qu'est un sous groupe engendré par la classe de 2....
En fait je connais la prop qui dit que H est un sous groupe de G ssi H est inclus dans G et quelque soit x et y appartenant à H alors x + y-1 appartient aussi à H
Mais concrètement je ne vois rien du tout. Même face à ma table. La seule chose que je remarque pour la classe de 2 dans la table de /6 c'est que l'addition de la classe de 2 avec elle même donne la classe de 4 et que la classe de 4 additionnée avec elle même donne 2 mais je ne sais même pas si ça à un quelconque sens dans ce qu'on fait là...