Inscription / Connexion Nouveau Sujet
structure du groupe diédral
Bonjour,je voudrais en faite comprendre la structure du groupe diédral.Le groupe diédral noté Dn, pour n
2, ou parfois D2n, est un groupe d'ordre 2n qui s'interprète notamment comme le groupe des isométries du plan conservant un polygone régulier à n côtés.Le groupe est constitué de n éléments correspondant aux rotations et n autres correspondant aux réflexions.Je ne comprend comment on détermine les images par la réflexion,par exemple soit D6,on note O le centre de ce polygone et Ai,i
{1,...,12} les cotés du polygone que vaut s(A1),on fait une symétrie par rapport à quoi?l'axe des abscisse?l'axe des ordonnées?
... si n est pair, on fait les symétries par rapport à chaque diagonale. S'il est impair par rapport à la droite qui passe par un sommet et le milieu du sommet opposé.
triangle équilatéral avec un sommet en A_0=(1,0). Les 6 éléments sont:
identité
rotation d'angle
rotation d'angle
symétrie par rapport à Ox
symétrie par rapport à la hauteur issue de
symétrie par rfapport à la hauteur issue de
Carré avec
identité
rotation d'angle
rotation d'angle (symétrie centrale par rapport à O)
rotation d'angle
symétrie par rapport à (axe Ox)
symétrie par rapport à (axe Oy)
symétrie par rapport à la première bissectrice
symétrie par rapport à la deuxième bissectrice
De toute façon, dans le cas général, le groupe est engendré par la rotation r d'angle et par la symétrie s par rapport à Ox (toujours si
) Vérifie que
est une symétrie.
Bonjour,
Les 6 axes des symétries de :
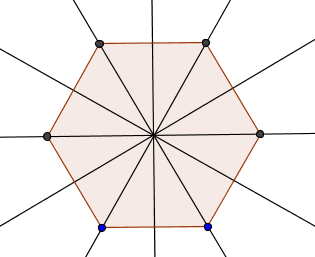
(Camelia, tu as oublié es axes joignant les milieux de côtés opposés dans le cas pair - il n'y a pas que les diagonales 
).
Annuler
connectez vous
algèbre en post-bac