Niveau Licence Maths 1e ann

Suite de fonctions L1(R) ne tendant pas vers 0

Posté par
LucileM4485 31-03-15 à 17:42

Bonjour à tous !

Alors voilà j'ai besoin d'un petit coup de main. On me demande de trouver une suite de fonctions fn L1([0,1]) telle que fn->0 dans L1 mais fn ne tend pas vers 0 presque partout.

On avait vu une suite de fonctions dans mon cours qui selon moi correspondrait, c'est une fonction qui correspond à des "carrés. En fait f0 vaut 1 sur [0,1/2] et 0 ailleurs, f1 vaut 1 sur [1/2,1] 0 ailleurs, f2 vaut 1 sur [0,1/4] et 0 ailleurs, f3 vaut 1 sur [1/4,1/2] et 0 ailleurs, en découpant l'intervalle en 2, puis en 4, puis en 8 etc.
Cependant, je n'arrive pas à expliciter la fonction, je n'ai que les dessins la représentant, j'ai donc besoin de votre aide pour l'expliciter s'il vous plaît Merci d'avance !

Posté par re : Suite de fonctions L1(R) ne tendant pas vers 0 31-03-15 à 20:36

Ton exemple est mal juger. Pour un, prendre par exemple un sin(nx).

Posté par re : Suite de fonctions L1(R) ne tendant pas vers 0 31-03-15 à 22:06

Bonsoir,
regarde l'ensemble de Cantor .

Une remarque de vocabulaire : si la suite (f_n) tend vers 0 pour la norme L¹ la limite est nulle « presque partout ». De mon temps c'était la définition de cette expression, et je n'ai pas entendu dire que ça ai changé.

Posté par Convergence en moyenne sans convergence simple 02-04-15 à 16:23

Je pense que dans l'exemple qui suit on a la convergence en moyenne sur $[0,1]$ sans convergence simple. Pour passer à $[-1,1]$ une extension par parité suffit.

Ce qui m'inquiète c'est la contradiction avec l'affirmation de verdurin concernant la convergence simple "presque partout" mais je me demande s'il n'a pas oublié de l'énoncer avec des suites décroissantes.

Je vous demande donc d'examiner avec soin ce qui suit, au cas où je me serais planté...

A chaque entier $p$ on peut associer un couple $(n,k)\in\N^2$ tel que $p=2^n+k,\;0\leqslant k<2^n$ (il suffit de prendre $n=E\Bigl(\dfrac{\ln p}{\ln2}\Bigr),\;k=p-2^n$ ).
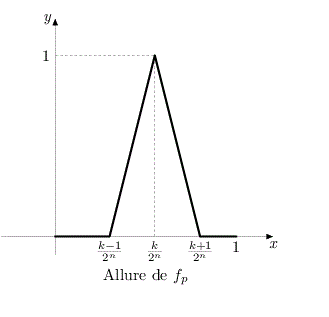
Soit alors $f_p$ définie sur $[0,1]$ par : voir schéma ci-dessous.
$\\ f_p(t)=\left\lbrace\begin{array}l \\ 0 \rm~~si~t<2^{-n}(k-1)~ \\ \\ 1-|2^nt-k|\rm~~si~|t-2^{-n}k|\leqslant 2^{-n}~ \\ \\ 0 \rm~~si~t>2^{-n}(k+1)~ \\ \end{array}\right. \\$
$f_p$ est continue et positive et (calcul d'aire de triangle) $\dsize\int_0^1f_p=\dfrac{k}{2^{2n}}<\dfrac2p$ . La suite $(f_p)_{p\in\N}$ converge vers 0 en moyenne.
Que se passe-t-il pour la convergence simple ? Soit $t\in[0,1],\;n\in\N$ .
Il existe un entier $k$ tel que $\dfrac{k}{2^{n+1}}\leqslant t<\dfrac{k+1}{2^n+1}$ .
Selon la parité de $k$ : voir les schémas.
Si $k=2q$ , $f_{2^n+q}(t)=1-(2^nt-q)=1-2^n\Bigl(t-\dfrac{k}{2^{n+1}}\Bigr)\geqslant1-\dfrac{2^n}{2{n+1}}=\dfrac12$
Si $k=2q-1$ , $f_{2^n+q}(t)=1-(q-2^nt)=1-2^n\Bigl(\dfrac{k+1}{2^{n+1}}-t\Bigr)\geqslant1-\dfrac{2^n}{2{n+1}}=\dfrac12$
Par conséquent la suite $p\mapsto f_p(t)$ admet une valeur d'adhérence supérieure à $\dfrac12$ .

Par ailleurs, pour $n\in\N^*$ , il existe $r,\;0\leqslant r<2^n$ tel que $f_{2^n+r}(t)=0$ donc $0$ est valeur d'adhérence de la suite $p\mapsto f_p$ .

Finalement il n'y a aucun point où la suite $p\mapsto f_p(t)$ converge.

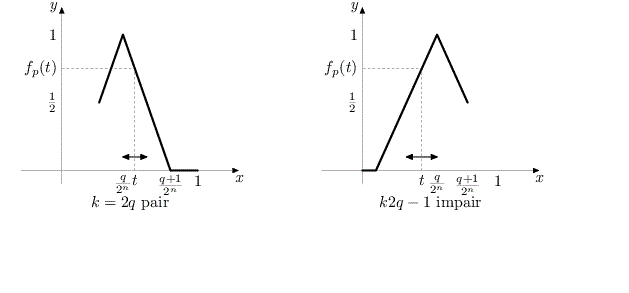
Convergence en moyenne sans convergence simple

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de maths

analyse en post-bac
21 fiches de mathématiques sur "analyse" en post-bac disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Cours et Exercices de maths

Forum de maths

college

lycee

Outils de maths

Pages les plus populaires

Suite de fonctions L1(R) ne tendant pas vers 0

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de maths