Inscription / Connexion Nouveau Sujet
Sujet du concours kangourou 2004 à resoudre....
bonjour...
je séche sur un pb du concours kangourou 2004 (j'ai la solution mais je ne comprend pas la methode...)
ce probléme comportant un figure, je vous joint donc le lien permettant d'y accéder : ***
il s'agit du pb n° 23...
merci par avance à ceux qui m'expliqueront le raisonnement..
Thioff
salut tu peux ecrire ton enonce
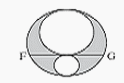
L'aire de la partie grisée sur la figure est égale à 2
Quelle est la longueur du segment [FG]
A)1
B)2
C)3
D)4
E)cela dépend des dimensions des 3 cercles
la figure peut être consultée sur le site Concours kangourou 2004
www.mathkang.org/pdf/juni2004.pdf
elle est aussi en piéce jointe...
la réponse est 4, mais comment y arrive t'on ?
Merci...
On a piR12+piR22=pi(R1+R2)2-2pi
EN développant on trouve R1*R2=1
Si j'exprime la puisance du cercle par rapprt au point de tangence intérieur on a :
(FG/2)2 = 2R1*2R2=4
FG2=4*4
FG=4
Merci à nofutur2 pour sa réponse, mais y a t'il une autre solution car en seconde je n'ai pas encore vu "la puisance du cercle par rapport au point de tangence intérieur" & je n'y comprend absolument rien malgré mes recherches sur ce sujet...
Les rayons des deux cercles inscrits sont R1 et R2 (avec R1>R2).
Le rayon du grand cercle (soit O ce point) est R1+R2.
La distance entre le centre du grand cercle et le point de tangance (soit A ce point) est égale à : (R1+R2)-2R2 = R1-R2.
D'après pythogore dans AOF donne OF2=2R1*2R2.
Donc OF=2* (R1*R2) = 2 (voir démonstration post précédente avec la différence des aires)
(R1*R2) = 2 (voir démonstration post précédente avec la différence des aires)
Donc FG=4.


