Étudies la fonction, tu verras par exemple que f() donc elle n'est pas surjective. De même tu verras si elle est injective ou non.

je l'ai étudié je trouve que son ensemble image  est compris entre -1 et 1.
Puis-je dire qu'elle est surjective ?
Comment montrer qu'elle n'est pas injective /qu'elle est injective ?

Étudies sa croissance (d'ailleurs tu peux te restreindre à [0,+[ pour l'étude étant donné que f est impaire). Tu verras que f croit puis décroit, donc elle va prendre la même valeurs en deux points différents, elle n'est donc pas injective sur R.

Après quand on parle de surjectivité/injectivité il faut préciser les ensembles.

Comme n'est pas surjective, par contre    l'est.

C'est pareil pour l'injectivité : n'est pas injective mais en se restreignant à un bon intervalle de départ, par exemple où y est strictement décroissante, est injective.

J'ai bien compris pour dire qu'elle n'est pas injective ( = au plus un antecedent) mais pour montrer qu'elle n'est pas surjective je fais comment ?
On a f:R --> R  
J'ai également montrer que f(R) = [-1;1]

J'ai pas bien compris ta phrase : " Comme f(R) = [-1;1], f:R-->R..." Comment tu sais qu'elle n'est pas surjective sur cet ensemble ?

Merci pour ton aide

f:A->B est surjective ssi tout élément de B à un antécédent par f dans A.

f:R->R n'est pas surjective par exemple car 2 n'a pas d'antécédent par f !

Par contre f:R->[-1,1] est surjective car tout réel de [-1,1] est "atteint" par f c'est-à-dire qu'il a un antécédent par f.

C'est plus clair ?

Oui c'est plus clair mais comment ta réussi à dire que 2 n'a pas d'antécédent par f ?
De plus, comment tu peux affirmer que tout réel de [-1;1] admet un antécédent par fois ? ( on peut pas tous les essayer.)

eh bien f(R)=[-1,1] ça veut dire que l'image par f de R est [-1,1] donc tout réel de [-1,1] a un antécédent par f, regarde le graphe de f pour t'en convaincre (étudier les variations de f permettent d'avoir le graphe)

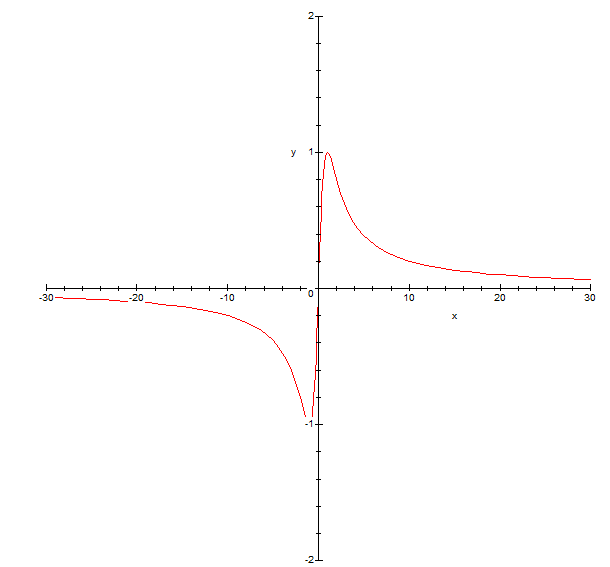
par exemple f est croissante sur [0,1], f(0)=0 et f(1)=1 donc f([0,1])=[0,1] par le théorème des valeurs intermédiaires (puisque f est continue)

Oui tu m'as convaincu merci. Donc la fonction f est surjective c'est bien ça ?

f:R->R n'est pas surjective mais f:R->[-1,1] est surjective.

Lorsqu'on parle d'une fonction f sans rien préciser, il est sous-entendu que c'est f:R->R dont il est question donc on peut effectivement dire que f n'est pas surjective.

D'accord merci.
Cette fonction f:[-1;1] -> [-1;1] est bijective. Comment je peux le montrer ?

Salut,

D'une pierre, deux coup :

Citation :
Soit (dans l'ensemble d'arrivé de ).

On a   si et seulement si  .

Alors donc

     # Si , le polynôme n'a pas de racine réelle, donc n'a pas d'antécédant et donc n'est pas surjective.
  
     # Si , le polynôme à deux racines donc a deux antécédents et donc n'est pas injective.

Voilà une solution plus élégante

_{coucou olive ça faisait très longtemps que je t'avais pas vu ^^}

J'aime beaucoup l'expression car elle a pleins de raccourcis dans le genre.. (par exemple si tu poses

_{Salut athrun, c'est d'ailleurs pour ça que je suis venu sur le topic, tu en ais où ? Ca se passe bien ?}

_es*

La classe ta méthode !

Avec cette méthode, je peux donc dire que sur [-1;1] f est surjective et injective, elle est donc bijective ?

Merci pour ton astuce.

f:[-1,1]->[-1,1] est bien bijective oui (f:[1,+oo[->]0,1] est aussi bijective)

_{je suis à Centrale Paris après avoir fait MP, et toi tu fais quoi maintenant ? j'ai cru voir que tu avais fait PCSI après MPSI}

Non. C'est pas bon.
Tout ce que tu peux dire c'est que est surjective. (Tu es toujours dans le cas de mon premier poste)
Il faut encore faire une réstriction de l'ensemble de départ pour avoir une bijection.
En fait, est bijective.
En effet, si , les racines sont tu remarques que en valeur absolue il y en a toujours une plus grande que 1 et une plus petite.

Mais je te laisse continuer avec athrun, ce que tu étais entrain de faire car il c'est la méthode de base qu'il faut savoir absoluement faire.

Désolé d'avoir dérangé ton travail athrun

_{Oh bg ! Bravo !!! Moi je suis sur CCP dans une école moyenne à Paris également, j'ai passé une partie de mes oraux chez toi d'ailleurs.}

Pas de soucis olive c'est intéressant ta méthode

_{Merci c'est quelle CCP exactement ?}

_{Supmeca, j'étais très proche d'avoir une INP (qui sont pas mal sur CCP) mais non ..
En tout cas, je suis très content pour toi. Grande classe serieux !}

olive_68  J'ai compris jusqu'à que x1,2 = 1 + ou - racine de (1-y²)/y.

A partir de là comment je peux déduire qu'elle est bijective ?

Merci

Tu sais que quelque soit la valeur de y, la racine avec un moins est toujours comprise entre [-1,1] et que la racine avec plus est dans le complément.
Donc dans [-1,1] il existe un unique racine, et donc bijectivité de f.

bonsoir
simplement
pour dire qu'on peut remarquer que pour tout x non nul donc f est non injective
et
pour dire bonsoir à Olive (j'ai failli arriver avant toi sur le topic des racines en cotan)

Bonsoir veleda

La classe, je me souvenais plus de cette invariance.
Je l'avais dit, elle est agréable cette fonction.

Aha, c'était une partie de questions d'un sujet CCP ou E3A que j'avais eus en DM et je l'avais eus en colle en sup, du coup j'ai encore tout en tête ^^

D'accord merci pour ta réponse, j'ai compris maintenant.