Inscription / Connexion Nouveau Sujet
tableau de variation
bonjour,
j'ai un exo trés long, et je coince sur un tableau de variation :
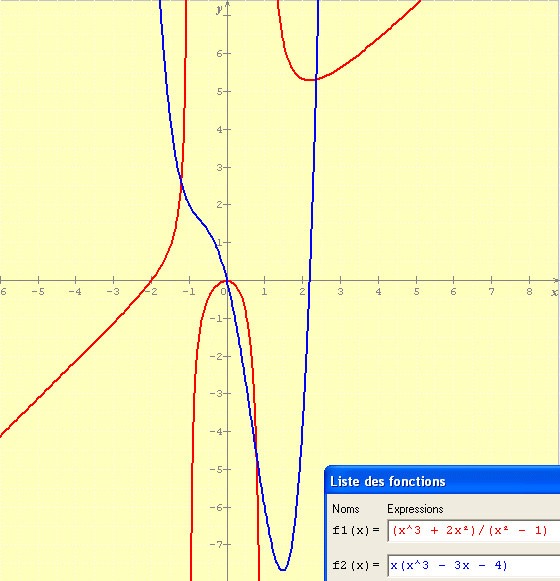
F(x) = x3 + 2x2 / (x2 - 1)
En dérivant j'obtiens :
F'(x) = x (x3 - 3x - 4) / (x2 - 1)2
Bien le dénominateur est toujours positif quelque soit x
Mais le numérateur je n'arrive pas à trouver quelque chose de cohérent
j'ai essayé des trucs mais je bloque (pas de racine évidente, ...)
merci
Bonjour.
Ton énoncé est bien : ?
Existe-t-il des questions précédentes dans lesquelles on te fait étudier x3 - 3x - 4 ?
A plus RR.
Bonjour 
Est ce que ?
Je trouve alors :
et je ne vois pas de racine évidente pour ! Est ce que ton énoncé est complet ?
on m'a demandé dans une question préalable d'étudier la variation de (x3 - 3x - 4) ce que j'ai fait en dérivant bien sûr
vu que tipoune93-1 semble bien mettre les parenthèses, je pense qu'il s'agit de :
f(x) = x3 + ( 2x²/(x² - 1) )

eh bien, si on t'a fait étudier les variations de x^3-3x-4, tu n'as plus qu'à le reporter dans le tableau de signes en ajoutant x puisque (x²-1)² est positif...

je te remercie mikayaou ma calculatrice m'a donnée l'allure du graphe mais je n'arrive pas à faire le DM qui m'est demandé c'est-à-dire ce tableau de variation car mes résultats son contraire au graphe
oui justement mon probleme est la j'ai bien pris en compte x et mes limites me donne le bon résultat par raport a la courbe que tu as dessiné. le probleme c'est que sur l'intervalle ]-oo, -1[ je trouve une fonction décroissante avec pour limite en -oo : -oo et en +oo: +oo. Donc je me suis forcément trompé quelque part car je devrai trouver une fonction croissante mais ce n'est pas le cas. C'est la raison pour laquelle ,j'ai besoin de votre aide.Merci
je ne comprends pas que...tu ne comprennes pas 
sur ]-oo,0[, f ' est positive et la fonction f est croissante... (ce qui confirme d'ailleurs que la limite en -oo valle -oo )
as-tu bien fait ton tableau de signes avec x et g(x) = x^3 - 3x - 4 ?

ba pour faire mon tableau j'ai pris la dérivée de g(x) car a mon niveua je ne sais pas faire un tableau x^3-3x-4, et il n'y a pas de solution evidente pour factoriser ceci. Alors comment as tu fait? Merci
bien voilà ou j'en suis :
g'(x) = 3(x2-1)
| x | -inf -1 0 1 +inf |
|------|-------------------------------------|
|g'(x) | + 0 - - 0 + |
|------|-------------------------------------|
| x | - - 0 + + |
|------|-------------------------------------|
|f'(x) | - + - + |
|------|-------------------------------------|
ici c'est faux
pourquoi ?