Inscription / Connexion Nouveau Sujet
Tableau de variation d'un volume
Bonjour, j'ai un exercice à faire, mais j'ai quelques difficultés, pourriez-vous m'aider.
ÉNONCÉ :ABCDEFGH est un cube d'arrête 8cm.
Pour tout point N de [AD] tel DN=AM.
On note AM=x (en cm).
Les droites (PM) et (NR) sont parallèles à (AE).
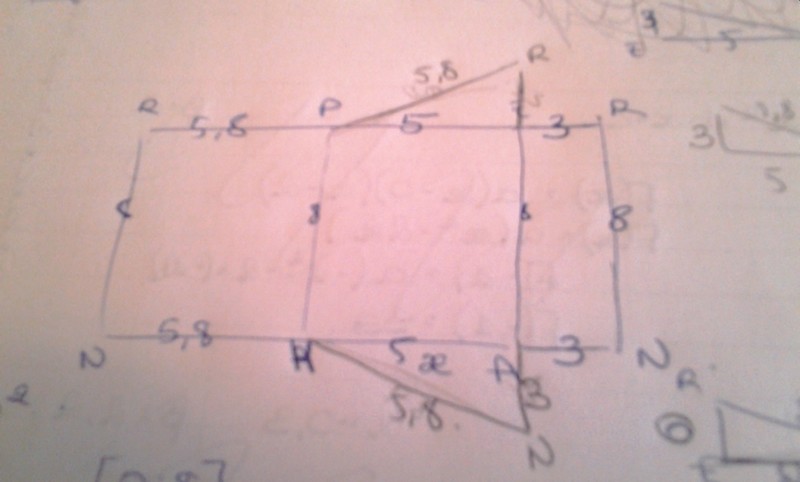
1. Réaliser un patron en vraies grandeurs du solide MANPER lorsque x vaut 5cm.
Donc j'ai fait le patron, je met en pièce jointe.
2. Exprimer le volume V(x) du solide MANPER en fonction de x.
Donc j'ai fait:
V=((3*5)/2)*8=60cm3.
3. Dresser le tableau de variations de V.
V admet il un minimum ou un maximum sur [0;8]?
Donner la valeur de cet extrémum.
Quelle est la position de M lorsqu'il est atteint?
J'ai essayer quelque chose mais je ne sais pas si c'est correct:
Lorsque le Volume est minimum, c'est lorsque x=0
V=((3*0)/2)*8
V=0
Et lorsque le Volume est maximum, c'est lorsque x=8
V=((3*8)/2)*8
V=96cm3
Donc je voulais savoir si c'était juste, je suis pas vraiment sûr. Pourriez-vous m'aider.
Bonjour Axelle17
Je suppose que la lettre qui ressemble à un "H" est un "M"...
Pour la question 2), l'énoncé demande le calcul de V(x) en fonction de x.
Ton calcul est basé sur x = 5, mais ce n'est qu'un cas particulier.
Néanmoins, tu as utilisé la bonne formule du volume.
La réponse correcte est donc : .
Pour la question 3), je te suggère de transformer l'expression de A(x).
Tu dois arriver à ceci :


