Bonjour

1°) Oui c'est bon

2°)
a) Que vas-tu faire une fois que tu as (2x-3)(2x-9) > -9 ? Tu penses que ça aide vraiment? Il ne me semble pas, car pour continuer, il va falloir tout mettre dans le même membre et développer... Quitte à faire cela, autant directement commencer avec la forme développée de f(x) !

En effet, 4x²-24x+27 > -9
cela donne en regroupant :
4x²-24x+36>0
Soit :
(2x-6)²>0 ce qui est toujours vrai quelque soit la valeur de x.

Continue.

Bonjour


Question 1 :  f(x) = 4x²-24x+27


Question 2 :  f(x) - 9
              4x²-24x+36 0
              4(x-3)² 0
et c'est juste vu que 4 et (x-3)² sont toujours positifs !


Question 3 :
               f(x) 0
               (2x-3)(2x-9) 0

Fais un tableau des signes et trouve sur quel intevalle le produit (2x-3)(2x-9) est positif !


Question 4 :  
                 f(x) 4x²
                 -24x+27 0
tu continues ..  (-24x+27 =0 puis tu trouves la solution.. )


Question 5 :      0 f(x) 4x²

Tu utilises les deux réponses précédentes !

bonjour nadou pour la question 3 le tableau de signe est le suivant:
    x    -inf     3/2      9/2     +inf
    2x-3    -       0        +       +
    2x-9    -              -  0       +
     P       +     0        -  0         +
    x app ]-inf,3/2]u[9/2;+inf[.
        

A Nightmare : Oui en effet j'aurai fais 4x²-24x+27 > -9
Mais j'aurai d'abord reécris (2x-3)(2x-9)> -9 . Jpensais que c'était mieux .

Merci à dellys et nanou.


Pour dellis . Merci beaucoup pour la question 4°) je ne savais pas justement qu'on pouvait faire sa ! Mercii

bonjour Nadou
voici une solution amusante pour 2°a
(2x-3)(2x-9) = (2x-6+3)(2x-6-3) = (2x-6)³-3³
comme (2x-6)² 0, l'expression -(3²) donc -9
pour 2°c
fais attention au changement de signe :
-24x+27 0; 24x-27 0; 24x 27; x 27/24
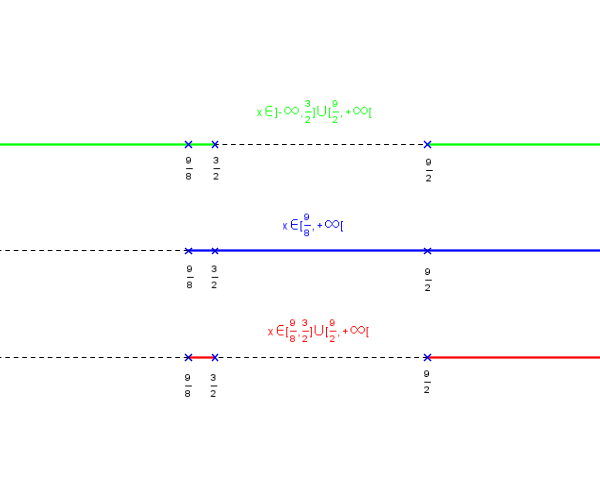
2°d : en combinant les réponses aux 2°b et 2°c :
x est dans [27/24;3/2] [9/2;+infini[

bonjour plumeteore je sis à la question 2)d et je vois ce que tu veux faire mais pourrais tu plus détayer silteplait je n'arrive pas à te suivre si tu vois ce que je veux dire..merci d'avance

réctification "je suis à la question 2)d"**^^

quelqu'un aurait il une reponse pour la dernière ?,je vois ce qu'il faut faire mais je ne sais pas l'apliqué...
merci d'avance pour vos rep

Bonjour,

Pour résoudre, l' inéquation: , tu dois utiliser les questions 2b) et 2c):

zut: oublie ce que j' ai ecrit au dessus

bonjour

_{...besoin d'un p'tit café toi aussi cailloux?}

Coucou,

>> Tokiohotel59

Un bon moyen pour déterminer des intersections d' intervalle est de faire un petit schéma.
Je te le prépare...

_{Oui Sarriette bien serré avec mes cachets}

<sub>cailloux > dans le même style et avec un schéma j'ai fait pire ce matin...

Je vous laisse bosser !</sub>

Voici ce que ça peut donner: (pas parfait...)

avec un schema s'est plus comprehensible^^merci à toi cailloux^^et tkt ton schema il est parfait