- Triangles : milieux et parallèles, théorème de Thalès
- Exercices sur les Triangles, milieux et parallèles
- Huit Exercices sur le théorème des milieux - quatrième
- 10 Exercices sur les équations et les mises en équations - quatrième
- Six Exercices sur les pourcentages - quatrième
- Cours sur les fractions suivis de six Exercices - quatrième
- Exercice de Calcul avec des fractions - 4ème
- Sept Exercices sur les fractions - quatrième
Inscription / Connexion Nouveau Sujet
triangle
Bonsoir a tous
STU est un triangle. i est le milieu de [TU]
La parallele a (Si) passant par T coupe (SU) en R et la parallele a(Si) passant par u coupe (ST) en V
A:demontrer que S est le mileiu de [RU] et de [TV].
B:en deduire la nature du quadrilatere RVUT
Merci pour votre aide
Bonsoir
shasha
As-tu fait un dessin ?
Pense à la droite des milieux dans un triangleet si 2 droites sont // à une même 3 ème elles sont // entre elles
voici un dessin possible
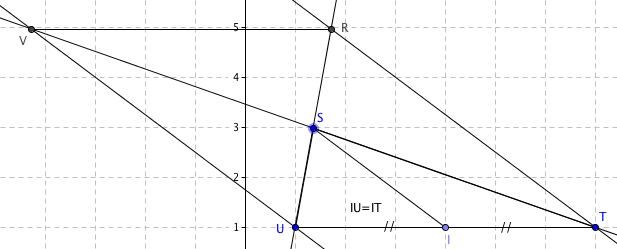
Bonjour à tous ! J'ai fais le dessin mais je n'arrive pas à demontrer que "s"est le milieu de [RU] et de [TV]
Pouvez vous m'aidez merci d'avance.
Si tu considères le triangle RUT, comme IU=IT et comme RT // SI, SI est la droite des milieux, donc S est le milieu de RU
fais le même raisonnement avec le triangle TUV, SI est encore la droite des milieux dans ce triangle
Pour le quadrilatère RTUV, RT // SI et UV // SI, donc RT // UV, et RT=2SI de même que UV=2SI, d'autre part les diagonales RU et TV se coupent en leur milieu S. Tu peux en conclure que le quadrilatère est un ?


