- Triangles : milieux et parallèles, théorème de Thalès
- Exercices sur les Triangles, milieux et parallèles
- Huit Exercices sur le théorème des milieux - quatrième
- 10 Exercices sur les équations et les mises en équations - quatrième
- Six Exercices sur les pourcentages - quatrième
- Cours sur les fractions suivis de six Exercices - quatrième
- Exercice de Calcul avec des fractions - 4ème
- Sept Exercices sur les fractions - quatrième
Inscription / Connexion Nouveau Sujet
Triangle et parallèles
Bonjour. J'aurais besoin d'aide pour un exercice en math sur les triangles, parallèles et cercles.
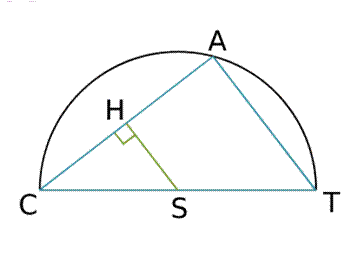
Dans la figure ci contre, le point A appartient au cercle de [CT] et le centre S. Les rdoites (HS) et (CA) sont perpendiculaires.
Montre que H est le milieu du segment CA.
Je n'ai pas compris, je sais juste que la médiane issue de l'angle droit mesure la moitié de l'hypothène. Mais est ce que ça va vraiment être utile: je ne pense pas...
Alors, pouvez mais au plus vite à résoudre cet exo.
Merci,
Lilina 
Le théorème de Thalès, tu connais ? ou la droite des milieux ?
Applique Thalès entre les deux triangles CSH et CTA
bonjour,
(HS) et (AT) sont perpendiculaires à la même droitr (AC)
donc HS et (AT) dont //
Appliquons chasles
CS/CT=CH/CA=1/2 ( puisque S est milieu de CT
A toi
Appliquons chasles
chasles était breton sans doute
 (en fait non, il est né à Epernon dans l'Eure-et-Loir) pauvre Thalès
(en fait non, il est né à Epernon dans l'Eure-et-Loir) pauvre Thalès 
Bonjour,
il ne faut pas oublier de justifier pourquoi on a l'angle droit en A ...
(et ensuite seulement comme vous avez dit)
de toute façon en 4ème Thalès s'appelle "droite des milieux" (Thalès c'est en 3ème)
bonjour,
ACT rec en A( théoreme du cercle inscrit)
(At) et (HS)  (AC)
(AC)
donc (AT)//(HS)
S milieu de CT par l'énoncé (le point A appartient au cercle de [CT] et le centre S.)
ds CAT, S milieu de CT,
(AT)//(SH)
si ds 1 triangle une droite passe par le milieu d'un coté et est // à un 2eme, alors elle passe par le milieu du 3eme,
donc H milieu de [CA]
On sait que S milieu de CT et H milieu du segment [CA]. Or si dans un triangle, , une droit passe par le milieu de deux côtés alors elle est parallèle au troisième côté. Donc les droites (HS) et (AT) sont parallèles.
Dans le triangle ACT, on sait que H appartient à CA, S appartient à CT et (HS) // (AT).
D'après le théorème de Thalès,
CS/CT = CH/CA = HS/AT c'est ça?
Voilà, j'ai appliqué le théorème des milieux et de Thalès, arrivé à la, peux tu me dire stp qu'elles segments on a besoin pour montrer que H est le milieu du segment [CA]? 
Mrc d'avance.
On sait que S milieu de CT et H milieu du segment [CA]
c'est ce qu'on cherche à démontrer ! tant qu'on ne l'a pas démontré on n'en sait rien.
lire la réponse détaillée de plvmpt
Bonjour merci pour toutes vos réponses. Si j'ai bien compris :
On sait que le triangle ACT est rectangle en A et que (AT) et (HS) (il ne faut pas le justifier ça??) perpendiculaire à la droite AC. Or si deux droites sont perpendiculaire à une même troisième alors elles sont parallèles entre elles. Donc les droites (HS) et (AT) sont parallèles.
De plus, on sait que le point A appartient au cercle de diamètre [CT]et le centre S. Donc S milieu de ST.
Dans le triangle CAT, on a S milieu de CT et (AT)// (SH). Or si dans un triangle une droite passe par le milieu dans côté et est parallèle à un deuxième côté alors elle passe par le milieu du troisième côté.
Donc H est le milieu du segment [CA].
Vérifiez si il n'y a pas de faute même des fautes de rédactions.
Merci plvmpt 
A est sur le cercle de diametre CT, or, si un triangle est inscrit dans un cercle et a pour côté un diamètre de ce cercle alors ce triangle est rectangle, donc ACT rectangle en A
(At) et (HS)  (AC),
(AC),
si 2 droites sont  à un ememe 3eme droite elles sont // entre elles,
à un ememe 3eme droite elles sont // entre elles,
donc (AT)//(HS)
on sait que CT est le diametre du cercle de centre S, donc S milieu de [CT]
dans le triangle rec CAT, on sait que
S milieu de [CT]
(AT)//(HS)
si dans un triangle une droite passe par le milieu d'un coté et est // à un 2eme, alors elle passe par le milieu du 3eme,
donc H milieu de [CA]
Merci de m'avoir posté la réponse. Mathafou enfait plvmpt à posté en même temps sa réponse que je n'ai pas pu voir puisque je venais de posté la mienne. Mais oui c'est vrai je ne suis pas très attentive..
Amicalement,
Lilina 
oui, on se demande pourquoi se décarcasser ...
mais lilina cherche peut être à démontrer le théorème du triangle inscrit dans un demi-cercle
théorème qui est tout de même vu en cours, donc qu'on applique sans devoir le redémontrer à chaque fois