Inscription / Connexion Nouveau Sujet
triangle isométrique
Bonjour,J'ai un exercice de math a faire pourriez-vous m'aider svp c'est a propos des triangles isométrique voici l'énoncé :
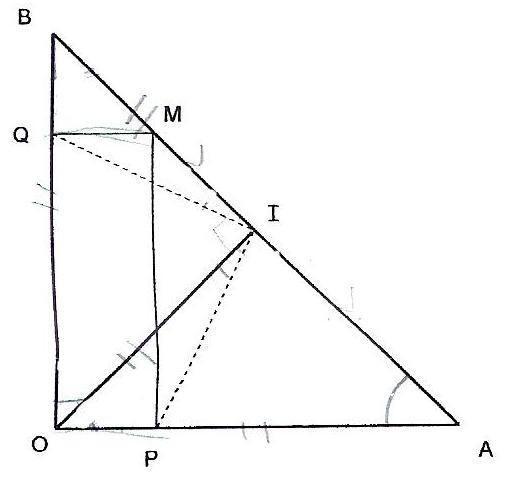
Dans cette figure,OAB est un triangle rectangle et isocèle de sommet 0.
I Est le milieu de [AB]
M Est un point de [AB] avec M # A ET M # B
Q est le projeté orthogonal de M sur (OB)
P est le projeté orthogonal de M sur (OA)
1) montrer que IBQ et IPO Sont isométriques.
[b][/b]Merci de votre aide =)
c une des propriété des triagle isométrique mais comen montrer que c des triangles isométrique aidez moi svp
Il faut d'abord chercher quel est l'angle de l'un des deux triangles dont on peut montrer l'égalité avec l'angle correspondant de l'autre triangle, en se servant des cas d'égalité des angles ( côtés parallèles ou perpendiculaires....).
Puis examiner les côtés adjacents à cet angle dans chaque triangle et démontrer les égalités, qui ressortent d'une analyse de la figure.
Essaie.
j'ai rien compris a ce que tu m'a dit quelqu'un ne peu pas m'aider plus je suis désespéré =s c'est un devoir a rendre é il est determinant de ma moyenne de math ='(
Je vais t'aider un peu plus.
Les deux angles dont je t'ai parlé sont les angles QBI pour le triangle IBQ et l'angle IOP pour le triangle IPO. Ils sont égaux car ils ont leurs côtés respectivement perpendiculaires: BQ perp. à OP et BM perp. à OI, par construction.
Par ailleurs, BM = OI, car, le triangle OAB étant rectangle en O, sa médiane OI est égale à la moitié BI de son hypothénuse AB.
Les autres côtés égaux sont BQ et OP. Cherche pour quelle raison on peut savoir qu'ils sont égaux......
Par ailleurs, BM = OI, car, le triangle OAB étant rectangle en O, sa médiane OI est égale à la moitié BI de son hypothénuse AB
Ce n'est pas BI=OI ?