Inscription / Connexion Nouveau Sujet
Triangle Rectangle Coordonnées Vecteur
Bonjour,
J'a un Devoir Maison à rendre et je bloque sur un exercice, j'aimerais que vous m'aidiez svp :
On considère ( O, I, J ) un repère orthonomé du plan.
Soit les points A(3;-2) B (7;2)et M(4;m) avec m qui appartient à R.
Determiner les valeurs de m pour lesquelles le triangle ABM est rectangle.
Merci de votre aide
Piki10
Bonsoir piki10
Tu calcules AB², AM² et BM² puis tu appliques Pythagore...
Il y aura 3 cas à envisager puisque l'énoncé ne dit pas qui est l'hypoténuse.
Petit rappel pour les distances :
Bonjour,
j'ai exactement le même DM de mathématique à rendre et même avec cette aide je n'y arrive pas.
je trouve des résultat incohérent et imcompréansible pour mon niveau pourriez vous m'aider
merci.
Bonsoir roots45
Commençons par la distance AB. Que vaut-elle ?
(Je vais devoir m'absenter une bonne heure...)
Il faudra revoir les calculs.
Il n'est pas utile de calculer AM, mais plutôt AM² pour utiliser le théorème de Pythagore.
J'avais rappelé la formule pour pouvoir calculer les carrés des longueurs.
Ainsi :
Tu refais ton calcul pour BM² ?
AH oui c'est ce que je me disais il y a un moins quelque part mais je ne sais ou ce qui fausse tout mon calcul merci et ensuite que dois je faire pour trouver m je ne vois pas.
Alors, là, tu as trois cas parce que l'énoncé ne signale pas quel est l'angle droit.
Si le triangle est rectangle en A, nous avons : BM² = AM² + AB².
Tu remplaces les trois valeurs par leurs correspondants.
Ainsi :
Tu résous cette équation...
Si le triangle est rectangle en B, nous avons : AM² = AB² + BM².
etc...
Si le triangle est rectangle en M, nous avons : AB² = AM² + BM².
etc...
Merci mais j'ai un problème pour les 2 premiers résultats normalement c'est bon:
Pour AM2=AB2+BM2 m=5
ensuite pour BM2=AB2+AM2 m=-3
mais pour AB2=AM2+BM2 je trouve un résultat incohérent:  4.
4.
Qu'ai-je mal fais?
Bonne soirée.
OK pour les deux premières réponses.
Ces valeurs conviennent puisque l'énoncé dit que .
Donc, no problem ! 
Attention je crois que vous avez faits une petite erreur d'inatention 13+5=18 et non 28 donc
cela fait - 7 ou
7 ou  7 mais cela me semble un peu bizarres
7 mais cela me semble un peu bizarres
car comment le reproduire sur une figure ?
Oups ! Quelle coquille ! 
Tu as raison pour les valeurs de m pour lesquelles une valeur approchée peut être trouvée par la calculatrice
Voici le dessin correspondant.
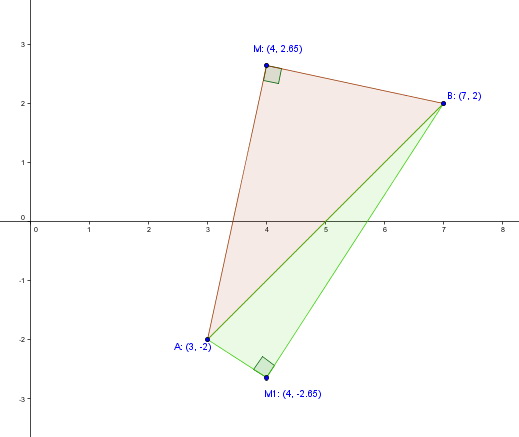
Merci pour la rectification. 
Et bien un grand merci à vous pour cet aide sur cet exercice merci d avoir donnée de votre temps pour moi
grace a vous j'ai enfn compris au revoir.



