Inscription / Connexion Nouveau Sujet
Trouver l'adhérence d'un ensemble
Bonjour, j'ai eu une liste d'exercice, dont l'un que je n'ai pas du tout compris ! Voici l'intitulé ;
Déterminer M (avec une barre au dessus) où
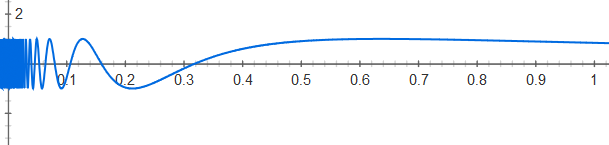
M = {(x,y) appartenant à R² | y=sin (1/x) , x appartient à ]0,1] }
(Ceci est le graphe d'une fonction)
Quelqu'un pour m'aider, s'il vous plait ?
Non, il faut que tu montres que tout élément de Mbar peut être approché par une suite d'éléments de M. Et que réciproquement, aucun élément en dehors de Mbar peut être approché par une suite d'éléments de M.
On a juste exhiber un ensemble. Pour la preuve il faut montrer que tout point est limite de suite de M et également comme tu l'écris que Mbar est un fermé. Pour le début c'est facile. pour fermé tu montres que c'est le complémentaire d'un ouvert. Tu prends un point qui n'est pas dans Mbar et tu montres qu'il existe une boule ouverte contenant ce point qui ne rencontre pas Mbar
L'adhérence M' de M est un fermé . C'est le plus petit fermé contenant M . C'est aussi l'ensembles des limites des suites convergentes à valeurs dans M .
.Ici tu penses que M ' = M 
{0}
[-1 , 1] .
Pour y arriver : tu montres que si y 
[-1 , 1] le point (0,y) est limite d'une suite à à valeurs dans M .
Comme tu as un dessin de M , regarde l'intersection de M avec une droite horizontale .
A ce stade tu auras montré l'inclusion M {0}[-1 , 1] 
M ' .
Il te restera à montrer l'inclusion inverse .
Rq : J'ai utilisé la notation X ' pour désigner l' adhérebce de X parce que c'est plus facile à écrire ( à taper ) .
Mais comme elle est utilisée par beaucoup pour désigner l'ensemble des points d'accumulation de X , il ne faut pas en abuser .
Annuler
connectez vous
topologie en post-bac