Bonjour à tous les insulaires des mathematiques, je viens vers vous car je n'arrive pas a me défaire de mon DM de maths que je trouve assez compliqué

C'est parti pour l'énoncé:

Dans tout ce probleme le plan euclidien est rapporté à un repere orthonormé (o,u,v).
On appelle birapport des 4 points A,B;C,D (dans cet ordre) 2 a 2 distincts et d'affixes complexes respectives a,b,c,d le nombre complexe égal à (c-a/d-a)*(d-b/c-b) et on le note [A,B,C,D]
Notations: (vect AB, vect CD) désigne l'angle orienté défini par les vecteurs AB et CD
Soient et deux reels.
On note = (modulo 2) s'il existe un entier relatif k tq =+2*k

1)Soient A,B,C,D 4 points 2 a 2 distincts et a,b,c,d leurs affixes complexes respectives

1)a) Montrer que arg[A,B,C,D]= (vect AD, vect AC) - ( vect BD, vect BC ) (modulo 2)


On a arg[A,B,C,D]= arg(c-a/d-a*d-b/c-b)= arg(c-a/d-a) + arg (d-b/c-b)
                                         = (vect AD, vect AC) + ( vect BC, vect BD)
                                         = (vect AD, vect AC) - ( vect BD, vect BC )

1)b) Démontrer que si A,B,C,D sont alignés alors [A,B,C,D] est un nombre reel.

A,B,C,D alignés arg [A,B,C,D]= 0 (modulo )

d'apres la question precedente: (vectAD, vect AC) + (vect BC, vect BD)= 0

arg [A,B,C;D]=0 donc [A,B;C,D] si ABCD alignés

Ici je suis pas tout a fait sur que le raisonnement se fasse de cette manière.

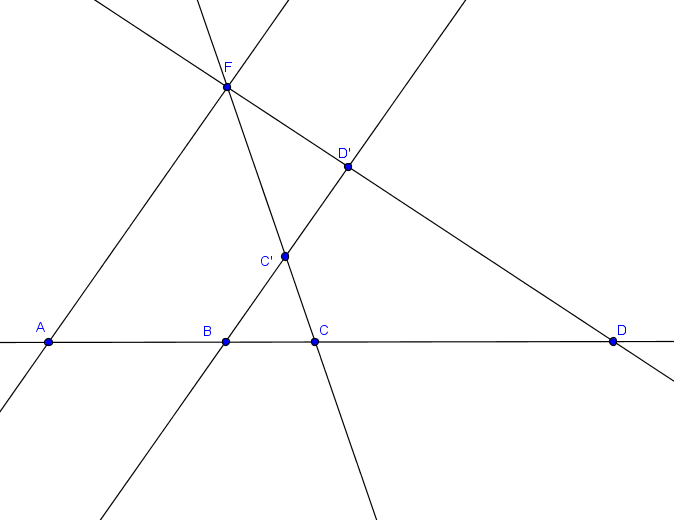
2) Dans cette question, on considere les points suivants:
A(1;0)  B(2,0)  C(4,0)  D(5,0)  F(0,3)

Soit (D) la droite d'équation y=x et soient A',B',C',D' les points définis par les intersections suivantes:
A'=(D)(FA)
B'=(D)(FB)
C'=(D)(FC)
D'=(D)(FD)

2a) Faire une figure et calculer la valeur du birapport [A,B,C,D]

Ici je remplace (c-a/d-a)*(d-b/c-b) par la valeur des coordonnees des points ABCD

Avec soit X la valeur du birapport et zX=(9/8;0)
Une nouvelle fois pas sur du resultat ici [/rouge

2)b) Calculer les coordonnées de A'

[rouge]Ici je fais un systeme avec les equations des deux droites (FA) et (D)
pour (FA) je me sert des 2 points de la droite et j obtiens y=-3x+3
La résolution du systeme donne A'(3/4; 3/4) ou 3/4(1+i)

2)c) Mq B' a pour affixe 6/5(1+i)

Meme principe que la question precedente et je trouve pareil.

2)d) on admet que C' a pour affixe 12/7(1+i) et D' a pour affixe 15/8(1+i)
          Mq [A',B',C',D']=[A,B,C,D]

Alors la apres avoir fait un calcul de 5 km je tombe pas sur la meme valeur que 2)a)
je trouve 729/640 pour info

Des pistes ?

On va cherccher par la suite a etablir un resultat general sur la conservation du birapport dans une telle configuration.
3) Dans cette question on va etablir le th de thales enoncé avec des nombres complexes

Soient A,B,C,B',C' 5 pts du plan tq A,B,C sont alignés, A,B',C' sont alignés et A,B,B' ne sont PAS alignés.
On note a,b,c,b',c' leurs affixes respectives.

A partir de la c'est le vide intersidéral je trouve plus rien ni meme la moindre piste

3)a) Démontrer que si il existe un reel k tq (c-a/b-a)=(c'-a/b'-a)=k alors (c'-c/b'-b)=k et (BB')(CC').


3b) on suppose (BB')(CC')
i) Justifier qu il existe des reels k tq (c'-c/b'-b)=k et (c'-a/b'-a)=k'

ii) Mq   c-a - k'*(b-a)= (k'-k)*(b'-b)

iii) En remarquant que le teme de gauche de l'egalité precedente est l affixe d un vecteur colineaire a vectAB et le terme de droite l affixe d un vecteur colineaire a vect BB',
Justifier que (c-a/b-a)=(c'-a/b'-a)=k

4) Dans cette question on veut etablir le resultat suivant:

Soient A,B,C,D 4 pts alignés 2 a 2 distincts et F un point n appartenant pas a la droite (AB). La parallele a (AF) passant par B coupe (CF) en C' et (DF) en D'.
Alors d'-b=k(c'-b) avec k=[A,B,C,D}
Autrement dit vect BD'= k* vect BC'

On considere les points A,B,C,D,F,C',D' comme dans l enonce ci dessus et on note a,b,c,d,f,c',d' les affixes respectives des points precedents.
On pose k=[A,B,C;D]

a) Faire une figure et mq (c-a/c-b)=k(d-a/d-b)

b) Justifier les egalites suivantes: (f-a/c'-b)=(a-c/b-c) et (f-a/d'-b)=(a-d/b-d)

c) En déduire que d'-b=k(c'-b)

Il reste encore 3 questions mais je vais vous les épargner.
J'espere que mon post est assez aéré et compréhensible, je suis preneur de tout indice ou début de piste pour résoudre mon probleme !

Merci !