Bonjour elhor,

Peux-tu nous donner qques indices pour cette intégrale ?

Un/des changement(s) de variable par ex.

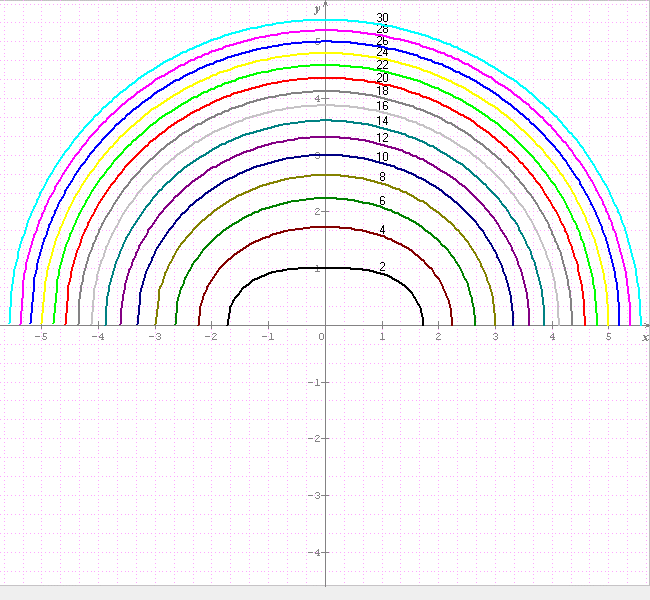
Par ailleurs, vu la nature des courbes C(alpha) qui s'apparentent à des arcs d'éllipse tendant vers le 1/2 cercle qd alpha ->oo, je pensais à :
- soit exprimer paramétriquement x(t) et y(t),
- soit l'exprimer en polaire r(théta),

cependant, je ne sais pas (plus?) calculer une intégrale dans ces cas-là

Philoux

Hum , c'est vrai que ça sens l'intégrale curviligne à plein nez , mais je ne vois pas quel changement en variable paramétrique faire . Peut être que je suis sur la mauvaise voie

>
pour rebondir sur mon post de 11:40, auriez-vous des liens intéressants et accessibles pour le calcul d'aire dans le cas d'expressions paramétriques ou polaires ?

Merci à l'avance

Philoux

Bonjour philoux,bonjour Nightmare:
Bien vu l'origine polaire de l'intégrale et pour plus de précision,elle provient de l'équation complexe: |z²-1|= ce sont à (moitié prés) les courbes que tu as déssiné philoux chacune d'elles délimite une surface valant 4*I.
Pour calculer I1 j'ai procédé par double changement de variable:
u=(1/2)[(4x²+1) - 1] puis u=cos(t) on trouve: I1=1/2
j'ai éssayé aprés de généraliser la méthode à I par le changement: u=(1/2)[(4x²+²) - ] mais la nouvelle intégrale n'est pas simple à calculer je continue à chercher

Bonsoir elhor

Ton équation me fait penser aux ovales de Cassini,

Avec >1, ton aire est égale à l'intégrale elliptique de deuxième espèce:

A = 2.1-^-2.sin²t dt

( bornes de l'intégrale de 0 à /2 )

Fabuleux elhor !

Continues de nous alimenter comme ça en nous donnant qques indices tout de même...

Aurais-tu une réponse à mon post de 12:18 hier ?

Merci

Philoux

_{Salut philoux et les autres, désolé de te déranger dans un topic où les maths sont au rendez-vous mais il faudra que tu songes à m'expliquer, envoi moi un mail si possible, merci}

Bonjour infophile,

Si dans ton mail tu as une explication dis moi-le.

C'est vrai qu'il y a une petite erreur dans mon résultat, car moi j'ai calulé sur les 4 cadrans, il suffit donc de diviser par 4 mon résultat.

Donc j'obtient:

I = /2 (1-^-2.sin²t)^0.5 dt

Je viens même de m'apercevoir que j'avais oublié d'écrire la racine du terme dans l'intégrale. ( est-ce ça qui te tracassé Philoux ?)

_{Marcfo: Je suis désolé mais ce n'est pas de cela dont je parlais , philoux comprendra de quoi . Encore désolé et bonne chance}

Bonjour elhor,

L'origine de ton problème connue, |z²-1|=r², (j'appelle ton lambda comme r² car il s'apparente à des produits de rayon, voir ci-dessous), je comprends mieux l'importance que semblaient avoir les points A(-1,0) et B(1,0) pour les courbes du post de 11:40.
A dessiner ces courbes, hormis celles pour 0<p<1 qui sont qqpeu particulières, ces deux points semblaient agir comme les foyers des "pseudo-ellipses" C(r²) et ton lambda semblait correspondre à l'excentricité e.

Si on écrit autrement l'équation complexe, on a :
|z²-1|=lambda=r² donc lambda positif puisque c'est un module => lambda=r²>0
|(z-1)(z+1)|=r²
|z-1|.|z+1|=r²
On recherche donc le lieu géométrique des points intersection de deux cercles centrés en A(-1,0) et B(1,0) et dont les rayons r1 et r2 sont tels que leur produit est constant et vaut lambda=r² : r1.r2=r²
Intersection de 2 cercles dont les centres sont symétriques/O(0,0) => figure avec deux axes de symétrie : Ox et Oy => Etude dans le premier quadrant et double symétrie (comme une ellipse).

Géométriquement, l'intersection maximale sera atteinte lorsque le rayon du plus grand cercle tangentera le plus petit.
Prenons r1>1 comme plus grand cercle, centré en A(-1,0) :
L'intersection maximale se produira sur Ox tel que (r1-1)=(1+r2) => r1-1=1+r²/r1 => r1²-2r1=r² => r1²-2r1+1=r²+1 => (r1-1)²=r²+1 => r1=1+V(r²+1) puisque r1>1. L'intersection se produira en x=r1-1=V(r²+1)=V(lambda+1)
Je comprends aussi mieux la borne supérieure de ton intégrale.

En revanche, ce que je ne parviens pas à m'expliquer c'est la signification géométrique/algébrique/autre? de ton intégrale.
Peut-elle correspondre à autre chose qu'un calcul d'aire pour lequel on s'excrime à trouver les bons changements de variables ?
Les bases théoriques me manquent pour exploiter cela...

Autre axe de recherche, toujours vis à vis de l'analogie des ellipses sur laquelle j'étais parti au début, l'équation polaire d'une ellipse est  r=k/( 1+e.cos(théta) ) avec e=excentricité; N'y aurait-il pas intérêt à exploiter cette forme pour rechercher ton intégrale I(lambda) ?
D'ailleurs, c'est ton calcul de I1 avec le deuxième changement u=cost qui me confirme cette intuition.
Là aussi, les bases théoriques (cf. mon mail de 11:47) me sont encore défaillantes...

Dernier axe : j'ai tenté d'approximer I(lambda) par régression linéaire et je trouve, avec un coef de corrélation linéaire de 0.999991, une droite I#(0.785)lambda (pour lambda entier>2).
Si cette intégrale est exprimable en fonction de lambda, et vu la valeur de I1=0.5<0.785, je pencherai vers du racine de lambda...

Tiens-nous au courant de tes recherches...

Philoux

Bonjour Philoux et elhor

Une bonne approximation de I est:

I=*/4*(1-1/(2²))^0.5

Quand pensez vous ?

Re-bonjour

C'est une approximation de la valeur exacte suivante:

A=./4.[1 - (1/2)².^-2 - ((1.3)/(2.4))².(^-4)/3 - ((1.3.5)/(2.4.6))².(^-6)/5 - ((1.3.5.7)/(2.4.6.8))².(^-8)/7  .....]

Ouf !

Salut.
Un truc à essayer dans ce genre de situations, c'est d'étudier I(), en étudiant notamment la continuité, la dérivabilité, une éventuelle parité etc.
Avec un peu de chance, on peut en tirer une équation fonctionnelle, voir différentielle, toujours intéressant à exploiter.

Quelqu'un a regardé dans cette voie?

C'est drole, à première vue on dirait que I"(t)=0, et que I(t)=Pi/4+1/2+sqrt(2)t/2 en regardant ca à la louche avec un logiciel de calcul.

Mais ca semble etre faux cependant, mais c'est une bonne approximation en tout cas.

Bonjour à tous les habitués de ce topic,

Intéressant de voir que ce sujet continue de vivre...

Merci marcfo pour le développement (17:20)
Ca tend à confirmer le 0,785 = pi/4 que j'estimais par RL.

Peux-tu nous dire comment tu es parvenu à cette somme infinie lambda.(pi/4)(1-Somme(Un)), de terme général Un :
(PI(2k-1)/PI(2k))²(lambda^(-2k))/(2k-1) , pour k=1 à n ?

Même question pour otto (21:54), comment es-tu parvenu à ce résultat ?

Bonne journée (ensoleillée à Paris, quel temps au Canada ?)

Philoux

Salut,
mon résultat je l'ai eu en tapant tout ca sous Maple, vu l'heure à laquelle j'ai posté, je ne suis pas fou (et je suis de passage en France)
Je vais essayer de regarder ca de plus près quand j'aurai un peu plus de temps.

Salut,

Moi pour mon résultat, comme je l'ai dit le 10 juin à 23h06,
Je suis parti de l'ovale de Cassini, qui m'a conduit à la résolution d'une intégrale elliptique de 2éme espèce.
Voilà, par ailleur Philoux je n'ai pas tous saisi de ta recherche,
(tu n'avais pas l'air d'adherer à mon résonnement ou alors je me trompe!).
Par contre Elhor qu'en penses-tu ?

L'approximation
A=*/4*(1-1/(2²))^0.5
devient trés vite correcte pour des valeurs de
Voilà

>marcfo

QUe nenni !

Ce n'est pas que "je n'adhérai à ton raisonnement", c'est surtout que "j'avais du mal à te suivre"

Je ne connais pas :
- les ovales (ovaux ?) de Cassini,
- les intégrales elliptique de quelque espèce que ce soit

Mais, grace à vos développements, j'essaie de suivre, d'où mes questions de béotien qui ne sont surtout pas critiques !

Donc, je te repose la question, qui est du 1° degré :
Comment arrive-t-on à cette expression avec Somme qui semble plus que correcte ?

Philoux

Philoux,

Rien de bien extra-ordinaire, j'ai juste fouillé sur le net, comment résoudre mon intégrale elliptique, elle paraissait pas bien compliquée mais je n'y arrivais pas. Je parle de l'intégrale du topic 11 juin à 14h27; j'ai trouvé donc un site sur les ellipses qui m'a bien aidé, .
A plus

>marcfo

merci pour le lien

Philoux

j'ai une intégrale a calculer ou plutot a touver sous la forme F=

                      int (cos²x) / racine(1+3cos²x)

voilà en vous remercient d'avance.

répondez vite svp

merci bonne chance