Cette formule est une véritable "passerelle" entre différents "univers" mathématiques.

Grâce à elle, tu peux établir une relation directe entre la trigonométrie, les nombres complexes, la géométrie, les exponentielles...

De nombreux problèmes peuvent se résoudre en utilisant ce passage. Lors d'un calcul ou d'une démonstration, tu peux en effet choisir le versant de la formule qui t'arrange le mieux.

D'ailleurs, à l'instant même où tu postais, il y avait une question posée dans le forum : Calculer (1+i)²⁰⁰⁷...
... qui se résout très facilement grâce à la formule d'Euler .

Bonjour Dino, et merci beaucoup pour ta réponse!

J'ai effectivement vu ce message concernant le ... et j'ai eu honte, mais je n'ai même pas su y répondre malgré mon travail sur la formule d'Euler! C'est vraiment triste et honteux de ma part. J'ai vu ça et je me suis dit que j'étais vraiment une pauvre cloche... pourtant dieu sait si j'aime les maths, malgré le fait que je n'y comprenne pas grand-chose.

D'ailleurs, toujours concernant ta réponse, aurais-tu quelques exemples concrets à me proposer? Dans la vie de tous les jours, à quoi sert cette formule? Je veux bien qu'elle serve à établir des relations entre trigonométrie, géométrie, etc... mais tout cela est un peu abstrait pour moi... je ne vois pas tellement à quoi tout cela peut servir... idem pour la résolution de ... quelle utilité trouver à ce genre de problèmes et à leur résolution?

Encore merci d'avance, de la part d'une pauvre nulle parfois (souvent même) désespérée par les maths...

Supradyn

Lol Supradyn !
Tu fais un concours d'humilité ?!?

Il n'y a pas de honte à avoir à ne pas savoir résoudre un problème mathématique. C'est avant tout une question de pratique et si tu avais l'occasion de t'exercer, tu ferais certainement des progrès, parce que le facteur de réussite numéro un, loin devant tous les autres, c'est la motivation.

Pour en revenir à ta question, calculer (1+i)²⁰⁰⁷ ne présente pas d'intérêt pratique évident en dehors de celui très concret de s'exercer à pratiquer ces notations afin de progresser... et accessoirement, de gagner l'estime du professeur .

D'autres applications de la formule d'Euler permettent de traiter par exemple des problèmes qu'on peut rencontrer en physique, dès qu'on s'intéresse notamment à des phénomènes périodiques. Par exemple, le comportement des circuits électriques en courant alternatif peut s'étudier très simplement grâce à ces notations.

Bonjour Suppradyn,

Tu sais sans doute que cosinus et sinus sont des fonction périodique de période .
Or donc est aussi une fonction périodique.

A quoi ça correspond dans le plan "complexe". En fait c'est un complexe de module 1 qui tourne dans le sens trigo lorsque x croît...
Si on considère que x est un temps, c'est en quelque sorte l'aiguille d'une pendule qui tourne (en sens inverse).

En fait on peut accélérer ou ralentir l'aiguille avec un terme réel...

est de période ou de fréquence .

de la même pour la fonction .

Remarque : Lorque est négatif on change de sens et lorque (resp. ) on ralenti (resp. accélère l'aiguille).

Mais plus intéressant, on on peut faire une somme de ses aiguille en les mettant bout à bout et en les faisant tourner les unes sur les autres.

On peut le voir ici .

En fait pour obtenir un cosinus il faut sommer deux aiguilles de même longueur qui tournent à la même vitesse mais en sens inverse:

.

remarque : Dans le lien ci-dessus, on projette sur un axe plutôt que d'ajouter l'aiguille "conjuguée".

La plupart du temps, on fait en fait le chemin inverse, et on cherche à partir d'une fonction à retrouver les "aiguilles tournantes" dont elle est la somme.

PS : En fait de somme finis, on a vite fait en mathématiques de passer au sommes infinies puis aux intégrales. Ça permet de décomposer des fonctions bien plus tordues.

Aspect pratique : On peut faire ça avec le son enregistré et c'est utile car notre oreille n'entend pas les son dont la fréquence est trop élevée ou trop grave. Ainsi, on peut enlever toutes ces "aiguilles" qui tournent trop vites ou pas assez et ça permet de gagner ééénormément de place sur notre disque dur.

On peut "compresser" les sons, mais aussi, les images ou les vidéos. C'est juste un peu plus complexe.

Pour recevoir la TNT, on utilise la modulation OFDM qui est basée sur cette même technique.

Dans les jeu vidéo et dans les films d'animation (pixar), on peut calculer les mouvement d'un fluide par des méthodes semblables.

Plein d'autres applications que j'oublie de mentionner...

ps2 : On parle de transformée de Fourier.
ps3 : A partir de l'image des aiguilles la plupart des propriétés sont intuitives...(, *)-morphisme...

D'accord, merci beaucoup pour ta réponse! Et ce n'est pas un concours d'humilité, non, c'est juste que j'ai parfois vraiment honte de mes connaissances en maths... et là plus particulièrement, puisque j'ai quand même passé une année à travailler sur la démonstration de cette formule sans savoir appris ni compris comment résoudre de problèmes avec... j'aimerais tellement en savoir et surtout en comprendre plus! J'ai de la motivation, mais le cerveau ne suit pas. Scumbag brain... ^^'

Sinon, j'ai essayé de résoudre sur le topic en question... sans succès, même avec tes indications. Peut-être pourras-tu m'éclairer une fois de plus?...

Finalement... encore un immense MERCI pour ta réponse et à bientôt!

Oulàlà... Matovitch, merci également pour ta réponse! Je n'ai pas encore tout lu, mais je vais m'y atteler et je te remercierai comme il se doit plus tard... en espérant que j'y comprenne quelque chose... tout cela m'a l'air fort compliqué.

Encore merci et à très vite!

Navré pour les nombreuses fautes d'orthographes.

Rebonjour, du coup!

J'ai bien lu tout ce que tu m'avais écrit Matovitch, encore merci! Cela dit... je n'ai pas compris grand-chose. À partir de "En fait on peut accélérer ou ralentir l'aiguille avec un terme k réel...", c'est un peu le désert pour moi... mais le sujet m'intéresse fortement, cependant.

Plus précisément, je n'ai pas compris:

- pourquoi la période de cos(kt) était égale à ?... Mais je n'ai pas compris non plus pourquoi on devait multiplier t par k pour accélérer ou ralentir le mouvement (dans le cas du cosinus, par exemple... je ne vois pas non-plus pourquoi k se retrouve dans l'exposant dans la fonction ) et je ne comprends pas non plus pourquoi la fréquence serait de ... si k est le facteur par lequel il faut multiplier t pour accélérer ou ralentir le "mouvement", pourquoi la fréquence consisterait à diviser k par ?

- idem pour la fonction ... je ne vois pas ce que k vient faire là-dedans ni comment il montre l'accélération/le ralentissement du "mouvement"... et soit dit en passant, je ne comprends pas non plus ce schéma (qui est me semble-t-il en lien avec ce dont nous traitons ici):



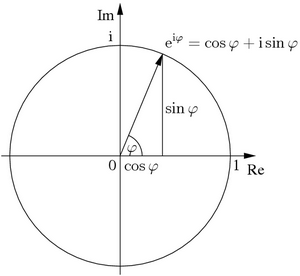
...car ne peut vraisemblablement pas être égal à ... non?

- je n'ai pas compris non plus comment on obtenait le cosinus en "faisant sommer deux aiguilles de même longueur qui tournent à la même vitesse mais en sens inverse"... ni pourquoi, visiblement on utilisait les expressions et pour faire intervenir ce "sens inverse"... pourquoi seul l'exposant devient-il négatif? Et pourquoi divise-t-on le tout par 2?

- Enfin... des aiguilles qui tourneraient plus vite, et donc dont le k serait plus élevée donnent des sons plus élevés (dans l'exemple "pratique")?... comment cela?

- Finalement... j'ignore ce que sont les intégrales et le morphisme... mais là, j'imagine qu'il s'agit encore d'une autre histoire...

Voilà pour mes questions concernant ta réponse, Matovitch... désolée pour toutes ces questions, je n'ai vraiment pas la lumière à tous les étages. Je ne pense pas que vous ayez le temps de répondre à toutes ces interrogations, mais s'il y en a quelques-unes, déjà... ce serait vraiment trop sympa de votre part. D'autant plus que le sujet m'intéresse vraiment et que quelques connaissances supplémentaires me seraient sûrement très utile d'ici très bientôt pour la présentation orale de mon travail...

Encore merci pour vos précédentes réponses, vos explications... et à très vite, peut-être (je l'espère!) pour de nouvelles réponses!

Supradyn

Et pas de soucis pour l'orthographe, Matovitch... il n'y a pas tant de fautes que ça!

Voici une vidéo très simple mais assez extraordinaire (à voir absolument) sur les complexes :

Bon, il faut savoir qu'un nombre complexe, ça se représente par un vecteur (accroché à l'origine) dans le plan.
On appelle d'ailleurs ce plan le plan complexe.

Exemple se représente par le vecteur de coordonnées .
par

On peut faire la somme de 2 nombres complexes :


Mais c'est pareil avec les vecteurs (on les mets bout à bout) :


On peut aussi en faire le produit :


Ça donne le vecteur .

Avec le produit il y a des trucs marrants qui se passent...

En effet, on définit le module d'un nombre complexe comme la norme des vecteurs.

exemple :

Ce qui est amusant avec le produit c'est que si et sont des complexes alors :
.

Par exemple or

Il y a un truc encore plus drôle mais ça concerne l'argument. L'argument qu'est ce que c'est ?
Il faut imaginer la demi-droite des réels positifs puis le vecteur accroché à l'origine.
Ça forme un angle orienté qu'on appelle argument.

Lorsqu'on fait le produit les arguments s'additionnent.

Par exemple l'argument de est .

On vérifie que à un argument de .

est le complexe de module et d'argument .
Lorque augmente, le vecteur tourne.

Si tu as compris toutes mes explications jusque là...tu devrais déjà mieux voir ce que je voulais dire.