Inscription / Connexion Nouveau Sujet
Valeur approché d'une série
Bonjour,
Je ne vois pas très bien comment résoudre cet exercice.
Je pensais à utiliser le critère intégral vu qu'on nous informe que c'est une fonction positive et décroissante.
Mais je ne vois pas par ou commencé .

Bonjour mathmusic,
Il s'agit d'un exercice très classique.
Pour la question 1.
Soit . Pour tout
, on a
puisque
décroît sur
. Donc
,
c'est-à-dire
.
Dans le cadre de cet exercice, seule l'inégalité
(I)
est utile. Ceci étant vrai pour tout les entiers naturels non nuls, tu devrais pouvoir en déduire :
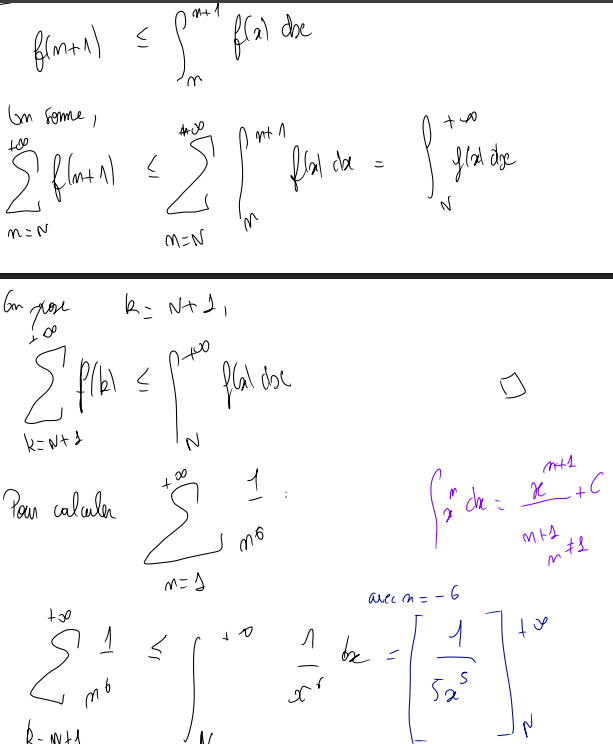
1. Pour tout ,
,
2. Pour tout ,
,
3. Que la série converge, puis, en reprenant ce qui a été fait précédemment en utilisant l'inégalité (I), tu devrais aussi pour voir en déduire l'inégalité demandée pour tout
.
Pour la question 2, une indication : l'hypothèse équivaut à dire que, pour tout ,
.
Tu devrais pouvoir en déduire que, pour tout ,
.
Soit , tu devrais alors pouvoir majorer simplement la somme
. Lorsque
tend vers
, ce majorant devrait tendre vers
. Rappelle-toi en effet que puisque
, on a

Petit rajout pour la suite, sur laquelle je ne me suis pas exprimé. Dans les deux cas, on demande une estimation de l'erreur obtenue à partir des inégalités prouvées.
Par exemple dans la question 1, pour , on te demande de calculer un nombre qui s'écrit
Pour avoir une précision donnée, il s'agit alors de choisir pour que ton erreur (que tu peux majorer par une intégrable calculable explicitement) soit suffisamment petite pour que tu sois sûre d'avoir 3 chiffres corrects après la virgule....
C'est la même idée dans la question 2
Bonsoir,
Dsl de répondre tard haha!
Merci beaucoup pour l'aide ! Je m'y pencherai demain . J'enverrai à quoi j'aboutis 
Bonne soirée et encore merci :
Bonsoir,
Je reviens vers toi te partager mes réponses .
En effet pour la partie calculatoire , il m'était impossible de le faire sans calculatrice ( à la main ça aurait bcp trop long ) .
Penses tu que ce soit raisonnable qu'on nous mette un exo de ce type (calculatoire sans calculatrice bien sur ) en partiel ?
Merci beaucoup pour ton aide , franchement ça ma beaucoup aidé j'aurais été perdue sans ça .


Bonjour mathmusic !
C'est pas mal ! Je vais néanmoins t'embêter un petit sur quelques points de rédaction 😊
En général quand on utilise des objets, il faut au préalable les introduire, question de rigueur. Par exemple dans le premier encadrement, qui est n ? Qui est x ?
On prendra soin d'écrire : pour tout , pour tout
, ....
Au tout début de ta deuxième image, tu déduis que ton integrale est majorée par M, mais ceci est vrai car f est positive, et il convient de le préciser !
Le theoreme que tu utilises, vous l'appelez "théorème de convergence monotone" ? Classiquement, je crois que l'on préfère le nommer "théorème de la limite monotone" car celui de la convergence monotone désigne plutôt un résultat de théorie de la mesure et de l'intégration. Bon, mais si vous lui donnez ce nom en cours, garde-le, cela me surprend juste un peu 😊
Bon. Je chipote un peu, c'est bien !

 )
)
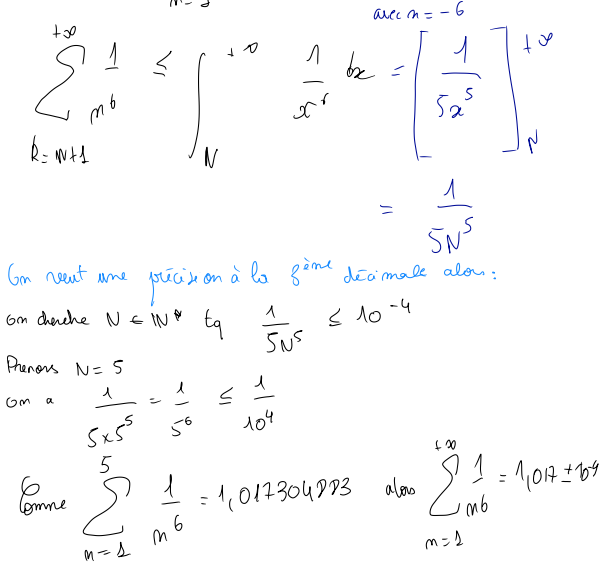

 analyse en post-bac
analyse en post-bac