Bonjour,
Un énoncé complet ainsi que des traces de tes recherches seraient bienvenus

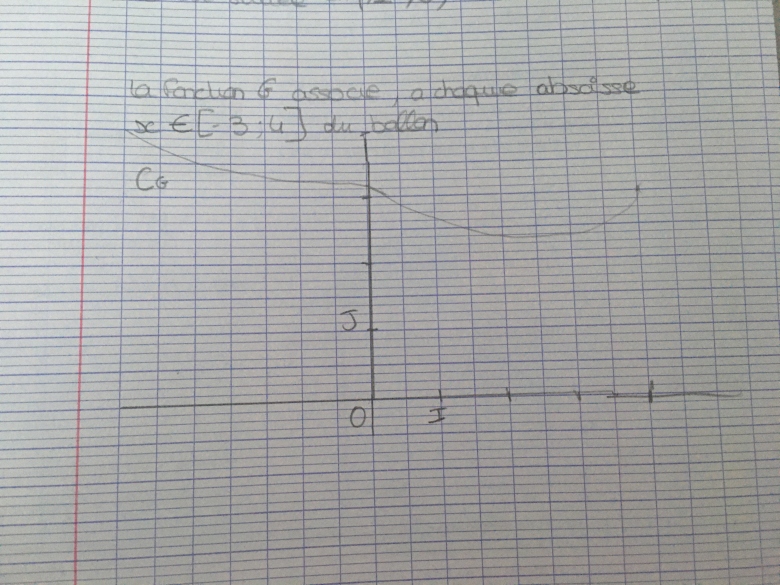
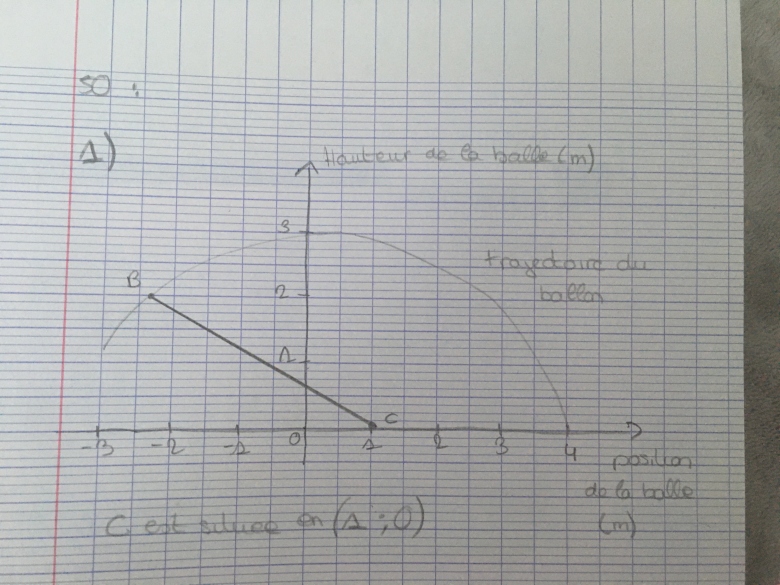
Bonjour le début de l'énoncé et celui ci on modélise la position d'une volleyeuse en utilisant un repère orthonormé du plan ainsi que la trajectoire du ballon. Une volleyeuse C est situé en ( 1:0)( position des pieds).

C'est ça ton énoncé?
C'est écrit comme ça?
On ne sait pas ce que c'est que G(x)

On nous dit que la fonction G associé à chaque abscisse x[-3;4] du ballon la longueur BC

C'est quoi BC?
On ne peut pas te répondre sans l'énoncé intégral!

Voici l?énoncé au complet

** image supprimée  conformément au point n° 3 de Sujet ancien- ne plus donner ce lien-merci
Tu dois recopier l'énoncé **

Tu proposes quoi alors pour démarrer ?

Si G est la fonction associé x[-3;4] alors G(0) a pour abscisse G(0)=(0;3,2)

Qu'il est impossible pour la volleyeuse de toucher le ballon

Lubna13,
tu devrais relire et appliquer les règles indiquées Sujet ancien- ne plus donner ce lien-merci

extrait de la FAQ du forum :

Q30 - J'ai été averti ou banni, pourquoi, et que faire ?

J'ai été averti ou banni parce que je n'ai pas respecté les règles du forum, qui étaient à lire avant de poster. et donc acceptées tacitement lors de l'inscription.

Ou bien j'ai un triangle rouge devant mon pseudo et je suis averti. Je peux réagir dès que je le désire, en m'engageant à respecter le règlement (une phrase à recopier), et je peux lever mon avertissement moi-même. Pour cela, je tente de répondre à mon message, et la procédure apparaît.
Un conseil cependant : vraiment lire le message "A lire avant de poster" et ne pas récidiver...Vous seriez alors banni.

Si je suis averti pour ne pas avoir respecté la manière de poster expliquée en Q05 , je relis Q05 , puis je lève mon avertissement et je reposte mon énoncé correctement cette fois, dans le même sujet, et ainsi j'obtiendrai de l'aide rapidement très certainement.

Ou bien ma figurine est masquée, j'ai été banni pour un certain temps, et je dois en attendre la fin.

Non dans certain cas la volleyeuse peut atteindre le filet au dessus de celui ci  de plus (1;0) est la position des pieds de la volleyeuse

Euhlair, je te remercie de ne pas répondre tant qu'un énoncé complet et recopié n'est pas donné par le demandeur
en effet, il est actuellement impossible de comprendre de quoi il retourne à la lecture de ces échanges

Bonjour j?ai un exercice en maths que je ne comprend pas pouvez vous m?aider voici l?énoncer



*** message déplacé ***

***attention, le multipost est strictement interdit sur notre site, et tu dois recopier ton énoncé comme déjà dit ***

Bonjour
Recopie ton énoncé.
Et
Poste tes graphiques seulement.

*** message déplacé ***