Bonjour,
Pour ces vacances j'ai un DM de maths à faire qui me pose problème... je vous laisse lire l'énoncé!
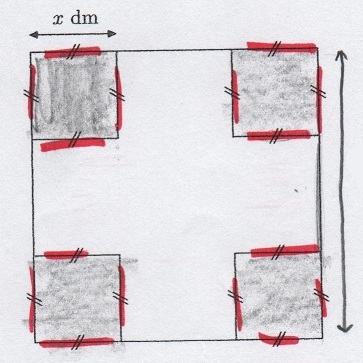
" Pour la construction de boîtes d'emballage, une usine décide de fabriquer des pavés droits. Pour cette fabrication, on utilise une plaque de métal carrée de 2 dm de côté ( sans épaisseur ). => voir figure.
On obtient le patron d'un pavé droit en découpant les parties grisées."
La question est : Pour quelles valeurs de x le volume de la boîte est-il maximal ?

Je sais que x varie dans l'intervalle [0;1]. J'ai cherché la fonction qui représente le volume de la boîte en fonction de x.. Cela m'a donné f(x)= 4x³-8x²+4x   ou   f(x)= 4x (x-1)².
En traçant la courbe représentative de cette fonction, je me suis aperçu que le point le plus haut avait pour coordonnées [ 1/3 ; 16/27 ].

Et c'est sur la validation que je bloque... Comment démontrer que pour tout x [0;1], le volume est inférieur ou égal à 16/27 ?

Merci de m'éclairer un peu.