Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Autres ressourcesTopics traitant de Autres ressources [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Fonctions

Posté par theo90 (invité) 10-09-07 à 22:14

J'ai ce DM à rendre pour Jeudi et j'ai d'énormes difficultés, pouvez-vous m'aider s'il vous plait.

Je vous montre ce que j'ai réussi à faire pour le moment:

Partie A:

Je suis parti du principe que T a pour équation y=4x+3
Donc y-3=4x

Donc, T passe par le point de tangence I de coordonnées (0;3) et a pour coefficient directeur 4.

Ici commence mon problème: f est dérivable sur R:

f'(x)= 6x+ax/2x
f'(x)= 3x + ax/2x

Donc f'(0) devrait être égal à 4 or, il est égal à 0 car 3*0 + a*0/2*0 = 0

Pouvez vous m'aidez s'il vous plait car j'ai retourné le problème dans tous les sens et je ne trouve rien du tout...

Après pour la partie B, j'ai de grosses difficultés...le vide total

Je vous remercie de votre aide.
                                                    

** image supprimée **

édit Océane : merci de faire l'effort de taper ton énoncé, l'attachement d'image étant réservé aux images

Posté par
cailloux Correcteurre : Fonctions 10-09-07 à 22:22

Bonsoir,

Il faut déjà que la courbe passe par I(0,3) soit \phi(0)=3=b

Après calculs: \phi'(x)=\frac{a(1-x^2)}{(x^2+1)^2}

et \phi'(0)=a=4

Finalement, \phi(x)=\frac{3x^2+4x+3}{x^2+1}

Posté par
cailloux Correcteurre : Fonctions 11-09-07 à 01:29

Re,

B -1) f(x)=\frac{3x^2+4x+3}{x^2+1}=\frac{3(x^2+1)+4x}{x^2+1}=3+\frac{4x}{x^2+1}

on a donc \alpha=3 et \beta=4

-2) f est définie sur \mathbb{R}.

Limites: \lim_{x\to -\infty}f(x)=\lim_{x\to -\infty}\frac{3x^2}{x^2}=3

de même: \lim_{x\to +\infty}f(x)=3

(C) présente donc une asymptote horizontale d' équation y=3 en \-\infty et +\infty.

Variations: f est dérivable sur \mathbb{R}

le A nous indique que f'(x)=\frac{4(1-x^2)}{x^2+1)^2}

f'(x)=0 pour x=\pm 1

sur ]-\infty,-1]\cup[1,+\infty[, f'(x)\leq 0 et f est strictement décroissante.

sur [-1,1], f'(x)\geq 0 et f est strictement croissante.

minimum local en -1 et f(-1)=1 maximum local en 1 et f(1)=5

-3) La tangente (T) en I(0,3) a pour équation y=4x+3

On étudie le signe de la différence:

f(x)-(4x+3)=\frac{4x}{x^2+1}-4x=-\frac{4x^3}{x^2+1}

Cette différence est du signe de -x^3 :

Donc sur ]-\infty,0], la courbe est au dessus de sa tangente en I

et sur [0,+\infty[ , la courbe est au dessous de sa tangente en I

La courbe traverse sa tangente en I; on dit que I est un point d' inflexion.

Centre de symétrie

Pour démontrer que I(a,b) est centre de symétrie d' une courbe représentative d' une fonction f, il faut prouver 2 choses:

\{\forall x \;\;a+x\in D_f \Longrightarrow a-x\in D_f\\\forall x\;\text{tel que}\;a+x\in D_f\;\;\frac{1}{2}[f(a+x)+f(a-x)]=b

Ici, D_f=\mathbb{R} et si x\in D_f, -x\in D_f

\frac{1}{2}[f(x)+f(-x)]=\frac{1}{2}\frac{3x^2+x+3+3x^2-4x+3}{x^2-1}=\frac{1}{2}\frac{6(x^2-1)}{x^2-1}=3

I(0,3) est donc centre de symétrie de (C).

-4) 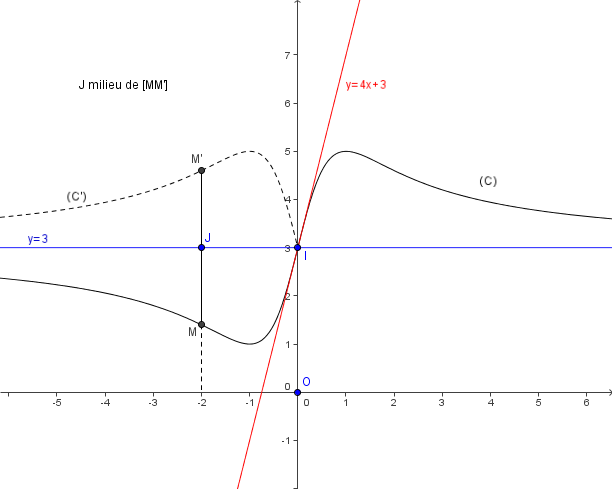Fonctions

-5) g(x)=\frac{3x^2+4|x|+3}{x^2-1}=3+\frac{4|x|}{x^2-1}

Si x\geq 0, f(x)=g(x) et les 2 courbes sont identiques sur \mathbb{R}^+

Si x\leq 0, g(x)=3-\frac{4x}{x^2+1}

sur ]-\infty,0], on a donc \frac{f(x)+g(x)}{2}=3 (1)

soit M(x,f(x))\in (C), M'(x,g(x))\in (C') et J(x,3) \in (D) (D) étant l' asymptote horizontale d' équation y=3

La relation (1) permet de dire que J est le milieu de [MM']

sur ]-\infty,0] on construit donc (C') image de (C) dans la symétrie d' axe (D)

Posté par
cailloux Correcteurre : Fonctions 11-09-07 à 01:41

Des erreurs de frappe:

Pour le centre de symétrie:

\frac{1}{2}[f(x)+f(-x)]=\frac{1}{2}\,\frac{3x^2+4x+3+3x^2-4x+3}{x^2+1}=\frac{1}{2}\,\frac{6(x^2+1}{x^2+1)}=3

Et après le graphe au 5), des dénominateurs en x^2-1 au lieu de x^2+1

Posté par theo90 (invité)Re 11-09-07 à 13:08

Merci beaucoup de ton aide, c'est cool ! Maintenant j'ai réussi à comprendre grâce à toi !!!

Posté par
cailloux Correcteurre : Fonctions 11-09-07 à 13:09

Bien content que tu aies compris!

Posté par
cailloux Correcteurre : Fonctions 11-09-07 à 13:11

Au fait, pour la dernière question, on pouvait " voir " aussi une symétrie par rapport à l' axe des ordonnées:

Pour x>0, \;\;g(-x)=f(x)

Posté par
touti62re 11-09-07 à 18:00

comment tu fais pour trouver la limite?

Posté par
cailloux Correcteurre : Fonctions 11-09-07 à 21:50

La limite d' une fraction rationnelle (un rapport de polynômes) à l' infini est la limite du rapport des termes de plus haut degré.


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !