Annuler
connectez vous
Autres ressources en terminale
- Un petit rappel de Cours sur le dénombrement - terminale
- Sept Exercices Q.C.M. sur le dénombrement - terminale
- Complexes, calcul vectoriel, problème - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. Reprise d'études-Ter Autres ressourcesTopics traitant de Autres ressources [tout]Lister tous les topics de mathématiques
Niveau Reprise d'études-Ter
Polynômes
Posté par pppa
Bonjour
Soit le polynôme de degré 3 P tel que P(x) = x^3+px+q Trouver les nombres a,b,c,d tels que l'on ait l'identité : P(x) = c*(x+a)^3 + d*(x+b)^3.
*
Par identification j'ai trouvé : c+d =1 ; bd = -ac ; a^2 c+b^2 d = p/3 ;
a^3 c+b^3 d = q et a+b = 3q/p
mais il faut exprimer chacun des nombres a, b,c et d en fonction de p et q.
Merci.
Citation :
Pourrais-tu nous dire comment tu as obtenu
?
Pourrais-tu nous dire comment tu as obtenu
Inutile : j'ai finalement vu que tu avais utilisé utilisé le système :
Ton résultat est correct.
>>Lake,
merci pour cette piste astucieuse. Je crois voir où l'on veut en venir, mais pour l'instant, après calcul et recalcul, je ne parviens pas à retrouver
Bonne soirée
Bonjour,
D'abord, relativement à ton exercice, remarquer en cours de calculs que le cas est à considérer à part.
On en tire
La solution s'élimine rapidement (elle correspond à
c'est à dire
)
On a donc
et
sont solutions de l'équation du deuxième degré :
Apparaît ensuite la plus ou moins célèbre quantité : ton problème n'a pas de solutions quand elle est négative.
En résumé, en supposant et
non nuls, ton exercice n'a de solutions que lorsque
c'est à dire lorsque le polynôme
a une unique racine (réelle).
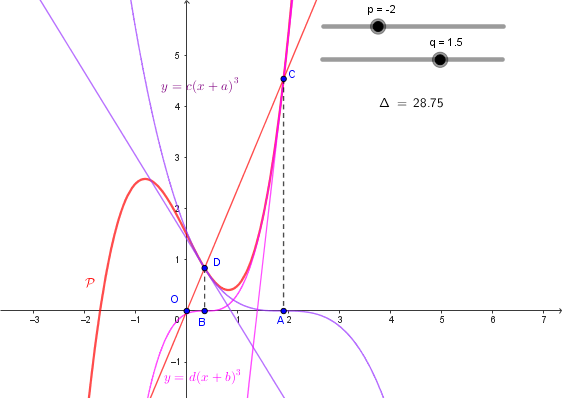
Sur cette figure (où ), on peut voir la courbe représentative du polynôme
, les courbes d'équations
et
, les points
et
d'abscisses
et
, 2 tangentes communes en ces points et l'alignement des points
.
Bonjour Lake,
merci beaucoup pour ton aide toujours aussi précieuse et efficace.
Tout est clair pour moi dorénavant quant à l'expression - si tant est qu'elle soit possible - de a,b,c, et d en fonction de p et q.
Reste un point sinon obscur, et tout cas un peu nébuleux. L'exercice invite à la fin
- à une discussion : j'avais pensé aux cas particuliers que tu avais évoqués : p = 0 (auquel cas l'expression de a+b n'aurait plus de signification)
et .
- Puis on demande de résoudre P(x) = 0 avec .
La quantité est négative, donc on ne peut pas exprimer a et b , a fortiori c et d, en fonction de p et q.
Avec , P a 3 racines, réelles... et pourtant elles semblent ne pouvoir s'exprimer qu'avec une écriture complexe.
Si je trace le graphe de P, il coupe l'axe des abscisses (l'axe des réels dans le plan complexe) par 3 fois . Si je résous P(x) = 0 avec dCode (logiciel solveur puissant en libre accès), j'ai 3 solutions, mais avec une écriture complexe, tandis que le logiciel qui trace le graphe me donne une valeur tronquée sur 2,3.....jusqu'à 9 décimales, sous une forme bien 'réelle', des trois 'zéros' de P.
Si tu le souhaites, et si tu as le temps, ça m'intéresserait d'avoir ton commentaire sur ce point.
Merci par avance.
En attendant, je vais essayer de traiter un exercice similaire un cran au-dessus, i.e. avec un polynôme de degré 4 (dont le terme de degré 2 est nul) ()
Il semble que nous ayons posté quasi en même temps.
Merci beaucoup pour ton message de 15h08, complémentaire du cas que j'ai évoqué.
Oui, hormis les cas nuls, la discussion principale repose sur le signe de
(voir au dessus).
Citation :
Avec
, P a 3 racines, réelles... et pourtant elles semblent ne pouvoir s'exprimer qu'avec une écriture complexe.
Avec
C'est la méthode de calcul qui le veut mais les sommes de complexes sont bel et bien réelles.
Historiquement, la méthode est due à Cardan (Méthode qu'il a plus ou moins volée à Tartaglia).
Voici un lien (si tu ne connais pas) :
En complément, je cite ce qui te chiffonne dans le lien:
Citation :
On peut noter que ce type de méthode met en évidence qu'il est parfois nécessaire de travailler dans un corps de nombres plus vaste que celui contenant les variables du problème pour trouver la solution : ici malgré le fait que les entrées (les coefficients) sont réelles, il faut passer par les complexes pour trouver toutes les solutions réelles.
On peut noter que ce type de méthode met en évidence qu'il est parfois nécessaire de travailler dans un corps de nombres plus vaste que celui contenant les variables du problème pour trouver la solution : ici malgré le fait que les entrées (les coefficients) sont réelles, il faut passer par les complexes pour trouver toutes les solutions réelles.
Citation :
L'utilisation des formules de Cardan nécessite parfois l'utilisation de nombres complexes, même pour trouver des solutions réelles. En fait, les nombres imaginaires sont précisément nés à cette occasion.
L'utilisation des formules de Cardan nécessite parfois l'utilisation de nombres complexes, même pour trouver des solutions réelles. En fait, les nombres imaginaires sont précisément nés à cette occasion.
Le lien Wikipedia, pour lequel je te remercie, je l'ai consulté à nouveau lors du traitement de cet exercice.
Sinon, sais-tu à qui revient la pater (ou mater) -nité de ces citations qui dissipent - un peu - ce brouillard 'réalo-complexe' ?
Encore merci
Philippe
Non, je ne sais pas mais en l'occurrence il s'agit d'"intervenants Wikipedia".
Il reste que ces notions sont relativement connues et n'ont plus rien de mystérieux aujourd'hui.
On est loin de l'époque des Cardan, Tartaglia, Bombelli ...
Juste une précision sans prétention au cas où tu repasserais par ici :
La droite a pour équation
Ce qui permet de faire une "construction" graphique via GeoGebra des points et
donc de leurs abscisses
et
