Annuler
connectez vous
autre en post-bac
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Ensemble et application Partie II
- Un best-of d'exos de probabilités (après le bac)
- Espaces vectoriels et Applications linéaires - supérieur
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Autre AutreTopics traitant de autre [tout]Lister tous les topics de mathématiques
Niveau autre
somme des carrés parfaits
Posté par shrodinger
Voici un exercice que le professeur de maths nous a donné pour les vacances:
Le 31 octobre 2008 , Sherlock Holmes entrait dans l'appartement avec agitation , me montrant un télégramme qu'il a reçu le matin même :
"Venez, Watson, il se trame encore quelque chose..."
La maison ou s'était déroulé le drame était pur le moins originale.La prémière pièce était de 1 m²,la deuxiéme de 2²,la troisième de 3² ... la dernière de 100².
Sherlock s'assit avec un papier et un crayon et me dit :
"Watson , l'aire totale de la maison vue de l'extérieur est de 338450 m², m'a dit Lestrade, et je trouve une aire totale de 338350 m².Une pièce de 100 m² a échappé aux policiers".
Sachant qu'il n'a posé qu'un calcul à la calulatrice, et que la méthode qu'il a utilisée est géométrique ,comment a-t-il fait ?
On pourra remarquer que 338350 = 100*101*201/6
Je n'arrive pas à résoudre cet exercice . Merci d'avance pour vos réponses!
édit Océane : merci de poser tes questions sur le forum adéquat
Conaissant mon prof , il veut la démonstration... de manière géométrique.(Forcément la démonstration algébrique se trouve facilement).
Bonjour !
Intéressant, je ne connaissais pas ce résultat !
Ouf, j'ai trouvé une solution, après une grosse prise de tête (hier).
Bon, tout d'abord j'ai essayé d'assembler des carrés dans le plan.
J'ai essayé de me baser sur le fait que un carré est la somme de nombres impairs, mais sans succès.
Puis j'ai vu que le numérateur était un polynôme de degrés trois, c'est ce qui ma fait penser au volume.
Là aussi, j'essaye d'assembler...mais rien. C'est alors que le 6 du dénominateur me fait penser à une pyramide :
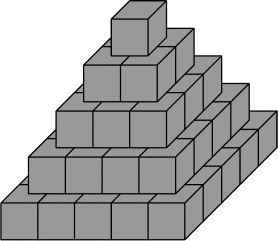
On calcule alors le volume de la pyramide extérieure :
Puis, on enlève ce qui dépasse sur les faces :
Et ce qui reste sur les arrêtes et au sommet :
On a donc :
Et on vérifie que
MV 
Euh, et ton prof l'a posé à toute la classe ??
Et sinon :
Citation :
Forcément la démonstration algébrique se trouve facilement
Forcément la démonstration algébrique se trouve facilement
Je suis curieux...
Je viens de trouver ce que tu cherches je crois : 
Dans visualisation des formules, somme des carrés.
MV
Bien vu pour la pyramide...
D'ailleurs pour les sommes des entiers, on peut le faire dans le plan :
****
.***
..**
...*
si a(n) est la somme des n premiers entiers, les jolis triangles ci-dessus montrent que :
Je pense qu'on peut le faire en dimension 4 en empilant des cubes pour trouver la somme des cubes.. Par contre pour les dessins...
Oui, j'ai aussi pensé à la dimension 4.
Mais, regarde le lien que j'ai donné pour la somme de cube :
333333
333333
333333
222333
222333
122333
Il y a un 1, huit 2, et vingt-sept 3.
d'où
MV
Merci pour vos réponses!(et surtout pour la tienne matovitch).Je n'aurais jamais pu trouver seul...
Pour la démonstration algébrique:
On remarque que la somme de k=1 à n de:(x+1)[/sup]3 -x[sup]3 est égal à (n+1)[/sup]3 -1
On développe (x+1)[sup]3 - x[sup][/sup]3 , et je te laisse faire les calculs...
Merci encore matovitch 