- Description de mathématique formelle-termes et relations
- Théorèmes
- Théories logiques
- Ensemble et application Partie II
- Équations différentielles : un Cours complet avec des exemples
- Un best-of d'exos de probabilités (après le bac)
- Espaces vectoriels et Applications linéaires - supérieur
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
Inscription / Connexion Nouveau Sujet
Théorie des ensembles
Bonsoir,
Soient A, B, C des parties d'un ensemble E. Dire si les propositions suivantes sont vraies. (Justifier vos réponses !)
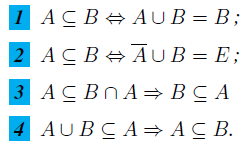
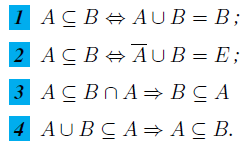
Bonsoir :juste une remarque supplementaire : tu ecris qu'une phrase a la meme signification qu'une egalité...???? Je vous laisse.
A est inclus dans B équivaut à dire que tous les éléments de A sont dans l'ensemble B. Donc l'ensemble des éléments appartenant à A ou à B est l'ensemble B.
et si tu finissais déjà celui-là : ![]() Égalité d'ensembles.
Égalité d'ensembles.
Salut,
Tu as deux implications à montrer :
La première :
On suppose que et tu dois montrer que
Pour montrer cette égalité, tu dois montrer la double inclusion puisque :
On suppose dit autrement on a
ou
, On a une disjonction de cas (2 cas), dans le premier cas on a
, l'hypothèse dit que
est dans
donc
est dans
, le second cas te dit directement que
est dans
, on conclut donc que
, on vient de montrer la premier inclusion.
Pour le reste, je te laisse finir avec la seconde inclusion.
La seconde : ()
On suppose que et on veut montrer que
Soit ...
Salut,
Puisque c'est un sujet qui date, je te donne un autre exemple détaillé pour t'aider à rédiger une preuve.
On veut montrer
______________________________________________________________________
On montre la première implication
On suppose que , et on cherche à montrer que
La première inclusion est triviale. Il nous reste à montrer que
.
Soit . On a soit
ou
, si
on a bien
, et si
, l'hypothèse nous dit que
est dans
, par conséquent
d'où
c'est à dire que
On conclut que puisque et
on a
______________________________________________________________________
On montre la seconde implication
On suppose que et on cherche à montrer que
Soit . Puisque
et que l'hypothèse nous dit que
, on déduit que
ou
or
n'est pas dans
puisqu'il est dans
, par conséquent il ne peut être que dans
d'où
______________________________________________________________________
On vient de montrer les deux implications par conséquent la proposition est vraie

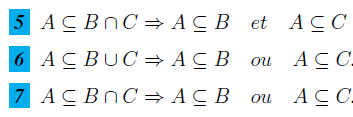



 logique en post-bac
logique en post-bac