- Fonction logarithme népérien, Cours de terminale
- Activités rapides sur les Fonctions logarithmiques
- Puissances d'un réel strictement positif (Terminale)
- Fonction exponentielle - Fiche de Cours terminale
- Le raisonnement par récurrence : principe et exemples rédigés
- Limites de fonctions - Cours sur les limites
- Fiche sur les nombres complexes - terminale
- Cours sur les suites en Terminale S
Fiche de mathématiques
Ile mathématiques > maths Tale > Fonction Logarithme
Révisez la fiche de cours sur les logarithmes
Déterminer les limites des fonctions suivantes aux bornes de leur ensemble de définition :
1.![f(x)=2x-\ln x \text{ définie sur } ]0;+\infty[](https://latex.ilemaths.net/latex-0.tex?f(x)=2x-\ln x \text{ définie sur } ]0;+\infty[)
2.![g(x)=\frac{x}{5\ln (x)} \text{ définie sur } ]1;+\infty[](https://latex.ilemaths.net/latex-0.tex?g(x)=\frac{x}{5\ln (x)} \text{ définie sur } ]1;+\infty[)
3.![h(x)=\frac{x}{-2+\ln x} \text{ définie sur } ]e^2;+\infty[](https://latex.ilemaths.net/latex-0.tex?h(x)=\frac{x}{-2+\ln x} \text{ définie sur } ]e^2;+\infty[)
1.=\ln (x^2-x+2))
2.=7\ln (x^2)+x^2)
Dresser le tableau de variations complet de la fonction définie sur
définie sur 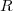 par
par =\ln (x^2+x+1))
}=\displaystyle{\lim_{\substack{x\to 0\\x>0}}2x-\ln x}=+\infty \text{ car } \displaystyle{\lim_{\substack{x\to 0\\x>0}}2x}=0 \text{ et } \displaystyle{\lim_{\substack{x\to 0\\x>0}}\ln x}=-\infty)
Limite au voisinage de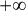
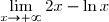 est une forme indéterminée du type
est une forme indéterminée du type 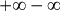 .
.
Or}{x})=+\infty \text{ car } \lim\limits_{x\to +\infty}\frac{\ln (x)}{x}=0 \text{ donc } \lim\limits_{x\to +\infty}2-\frac{\ln (x)}{x}=2)
2. Limite au voisinage de 1+
}=\displaystyle{\lim_{\substack{x\to 1\\x>1}}\frac{x}{5\ln (x)}}=+\infty \text{ car } \displaystyle{\lim_{\substack{x\to 1\\x>1}}x}=1 \text{ et } \dislpaystyle{\lim_{\substack{x\to 1\\x>1}}\ln (x)}=0^+)
Limite au voisinage de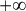
=\lim\limits_{x\to +\infty}\frac{x}{5\ln (x)}) est une forme indéterminée du type
est une forme indéterminée du type 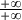
Or}{x}}=+\infty \text{ car } \lim\limits_{x\to +\infty}\frac{\ln (x)}{x}=0^+ \text{ donc } \lim\limits_{x\to +\infty}\frac{1}{\frac{\ln (x)}{x}}=+\infty)
3. Limite au voisinage de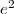
}=\displaystyle{\lim_{\substack{x\to e2\\x>e^2}}\frac{x}{-2+\ln x}}=+\infty \text{ car } \displaystyle{\lim_{\substack{x\to e^2\\x>e^2}}x}=e^2>0)
et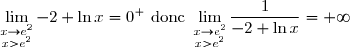
Limite au voisinage de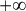
=\lim\limits_{x\to +\infty}\frac{x}{-2+\ln x}) est une forme indéterminée du type
est une forme indéterminée du type 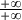
=\lim\limits_{x\to +\infty}\frac{e^{\ln x}}{-2+\ln x}=\lim\limits_{X\to +\infty} \frac{e^X}{-2+X}) en posant
en posant 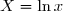
}=\lim\limits_{Y\to -\infty}\frac{e^{2-2Y}}{-2Y}) en posant
en posant 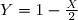
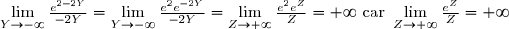
1.=\ln (x^2-x+2))
La fonction définie par
définie par =x^2-x+2) est définie et dérivable sur
est définie et dérivable sur 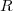 comme fonction polynôme du 2nd degré.
comme fonction polynôme du 2nd degré.
La fonction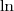 est définie et dérivable sur
est définie et dérivable sur ![]0;+\infty[](https://latex.ilemaths.net/latex-0.tex?]0;+\infty[)
Étude du signe de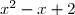
^2-4\times 1\times 2=1-8=-7<0) donc le trinôme du second degré est du signe de
donc le trinôme du second degré est du signe de 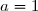 coefficient des
coefficient des 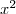 pour tout réel donc strictement positif.
pour tout réel donc strictement positif.
Ainsi, la fonction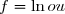 est définie et dérivable sur
est définie et dérivable sur 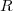

=\frac{2x-1}{x^2-x+2})
2.=7\ln (x^2)+x^2)
La fonction définie par
définie par =x^2) est définie et dérivable sur
est définie et dérivable sur 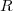 comme fonction polynôme du 2nd degré.
comme fonction polynôme du 2nd degré.
La fonction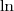 est définie et dérivable sur
est définie et dérivable sur ![]0;+\infty[](https://latex.ilemaths.net/latex-0.tex?]0;+\infty[)
Or
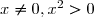 donc la fonction
donc la fonction 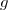 est définie et dérivable sur
est définie et dérivable sur 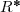

=7\times \frac{2x}{x^2}+2x=\frac{14x}{x^2}+2x=\frac{14}{x}+2x)
3.=\ln (\frac{3-x}{3+x}))
 définie par
définie par =x^2+x+1) est définie et dérivable sur
est définie et dérivable sur 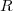 comme fonction polynôme du 2nd degré.
comme fonction polynôme du 2nd degré.
La fonction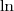 est définie et dérivable sur
est définie et dérivable sur ![]0;+\infty[](https://latex.ilemaths.net/latex-0.tex?]0;+\infty[)
Étude du signe de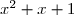
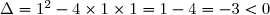 donc le trinôme du second degré est du signe de
donc le trinôme du second degré est du signe de 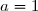 coefficient des
coefficient des 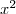 pour tout réel donc strictement positif.
pour tout réel donc strictement positif.
Ainsi, la fonction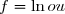 est définie et dérivable sur
est définie et dérivable sur 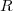
Limite au voisinage de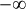
=+\infty) par composition des limites
par composition des limites
=\lim\limits_{x\to -\infty}(x^2)=+\infty \text{ et } \lim\limits_{X\to +\infty}\ln (X)=+\infty)
Limite au voisinage de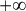
De même=+\infty) par composition des limites
par composition des limites
=\lim\limits_{x\to +\infty} (x^2)=+\infty \text{ et } \lim\limits_{X\to +\infty} \ln (X)=+\infty)
Dérivée de

=\frac{2x+1}{x^2+x+1})
Tableau de variations de
Comme
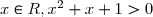 on déduit que
on déduit que ) est du signe de
est du signe de 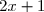
On a=\ln (\frac{1}{4}-\frac{1}{2}+1)=\ln (\frac{3}{4})=\ln 3-\ln 4)
 & & - & \barre{0} & + & \\ \hline \niveau{2}{3} f & +\infty & \decroit & \ln 3-\ln 4 & \croit & +\infty \\ \hline \end{tabvar})
Activités rapides sur les Fonctions logarithmiques - Volume 2
Révisez la fiche de cours sur les logarithmes
Enoncés
Exercice 1
Déterminer les limites des fonctions suivantes aux bornes de leur ensemble de définition :
1.
2.
3.
Exercice 2
Pour chacune des fonctions suivantes, étudier sa dérivabilité puis calculer sa dérivée :1.
2.
Exercice 3
Dresser le tableau de variations complet de la fonction
Exercice 1
1. Limite au voisinage de 0+Limite au voisinage de
Or
2. Limite au voisinage de 1+
Limite au voisinage de
Or
3. Limite au voisinage de
et
Limite au voisinage de
Exercice 2
Pour chacune des fonctions suivantes, calculer sa dérivée :1.
La fonction
La fonction
Étude du signe de
Ainsi, la fonction

2.
La fonction
La fonction
Or


3.
Exercice 3
La fonctionLa fonction
Étude du signe de
Ainsi, la fonction
Limite au voisinage de
Limite au voisinage de
De même
Dérivée de

Tableau de variations de
Comme

On a
ceci n'est qu'un extrait
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter

 Voir l'énoncé seul
Voir l'énoncé seul