Annuler
connectez vous
- Produit Scalaire dans l'espace - Cours terminale S
- Produit Scalaire dans l'espace - Exercice Terminale S
- Onze Exercices divers sur les vecteurs - première
- Fonction exponentielle - Fiche de Cours terminale
- Le raisonnement par récurrence : principe et exemples rédigés
- Limites de fonctions - Cours sur les limites
- Fiche sur les nombres complexes - terminale
- Cours sur les suites en Terminale S
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Produit scalaireTopics traitant de produit scalaire [tout]Lister tous les topics de mathématiques
Niveau terminale
ABCDEFGH un cube
Posté par Rachmaminoff
Bonjour.
J'ai un exercice qui me pose problème, je n'arrive pas a le résoudre. Je vous propose l'énoncé voir si on peut en discuter.
Soit ABCDEFG un cube d'arête 1. ( la figure n'est pas a la bonne échelle).
On pose et
Le bute de l'exercice est en fait de determiner a et b pour que (MN) soit perpendiculaire a (AF) et (BD), mais il faut utiliser deux methodes.
1) Le repère ortho (A,AB,AD,AE), et les coordonnées des points.
2) En décomposan
Pour la question 1, j'ai commencé en disant que si deux vecteurs sont orthogonaux, alors vec.vec=0
Donc
et
et
Mais en fait a partir de la je sais pas très bien comment m'en sortir j'ai esseyé des trucs au brouillon sans succès.
Voici la figure plus clairement.
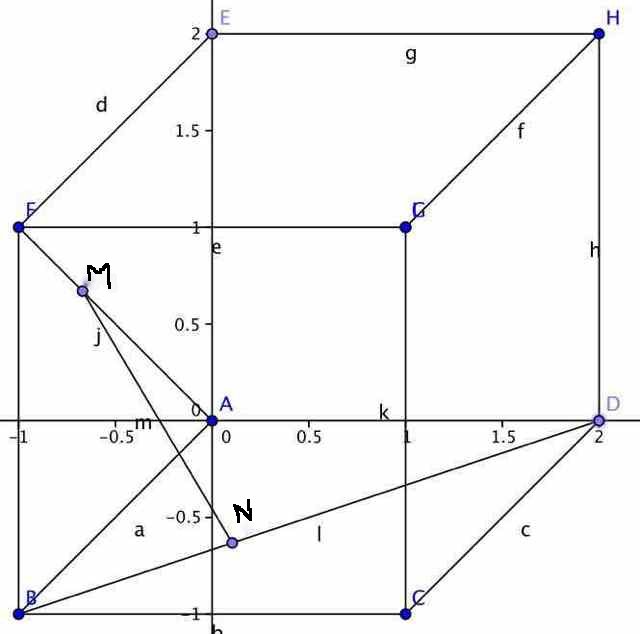
désolée mais pour ta figure dans l'espace, tu as utilisé un logiciel de géométrie plane; ton schéma est ainsi peu lisible; dommage!
au 1) je suppose que tu dois trouver a et b en utilisant le repère orthonormé (A; AB, AD, AE)
_il faut donner les coordonnées des points A, F, B, D, et établir les coordonnées des points M et N
_ calculer le produit scalaire des vecteurs MN et AF d'une part et MN et BD d'autre part
On en déduit deux équations à deux inconnues (puisque ces produits scalaires sont nuls)
au 2) il faut calculer les produits scalaires en utilisant les décompositions données dans l'énoncé et en développant etc.
bonsoir RACHMAMINOFF,
voici un chemin qui pourrais t'aider à résoudre ton problème.
Premièrement,trouves les coordonnées des points B,F,D,M,N dans le repère donné.
REMARQUE:la relation entre les vecteurs AM et AF montre que les coordonnées de M font a fois les coordonnées de F.
on a le vecteur BN qui est egal à la somme des vecteurs BA et AN (relation de CHARLES).en remplaçant le vecteur BN par cette somme dans l'égalite entre BN et BD,puis en faisant passer le vecteur BA du cote de l'é[url][/url]galite ou se situe le vecteur BD,on obtient le vecteur AN est égal à la somme des vecteurs AB et bBD ,ce qui nous donne les coordonnées du point N.
maintenant essaies de traduire MN.AF=0 et MN.BD=0 avec les coordonnées de ces différents vecteurs.tu obtiendras un système de deux équations contenant l'un a et l'autre b que tu vas résoudre pour obtenir la valeur de a et celle de b.
N.B:dans ce message considère les distances comme des vecteurs
j'espére que ce message t'auras aidé.