Inscription / Connexion Nouveau Sujet
Aire d'un rectangle inscrit dans un triangle
C'est possible que quelqu'un m'aide à propos de cette exercice :
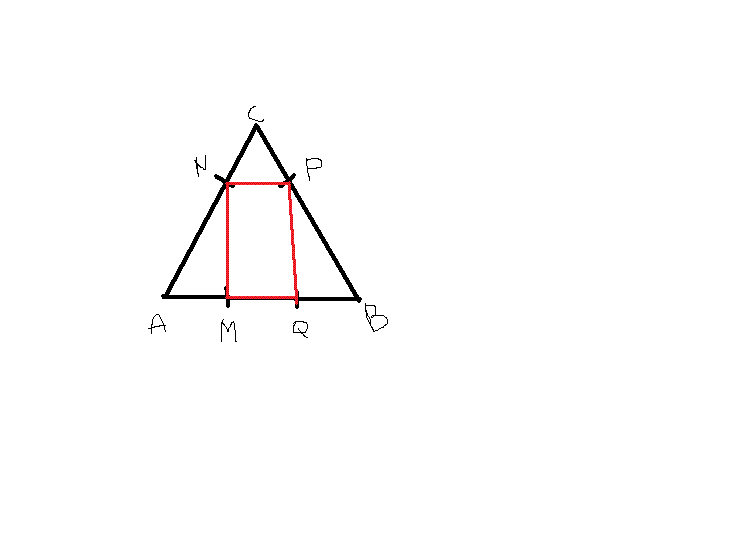
Soit ABC un triangle équilatéral de côté 8. On inscrit dans ce triangle un rectangle MNPQ avec N € [AC], P € [BC], M € [AB] et Q € [AB].
1) On pose x = AM et on désigne par a(x) l'aire de ce rectangle MNPQ.
a) Quelles sont les valeurs possibles de x ?
b) Calculer CH, H étant le pied de la hauteur issue de C.
c) Exprimer MN en fonction de x.
d) Montrer que a(x) = -2"racine carré"3 (x-2)"au carré" + 8"racine carré"3.
2)Pour quelle valeur de x l'aire est-elle maximale?
Merci 
tu peux regarder ici pour la premiere questio:
Aire d'un rectangle inscrit dans un triangle
1a) x est sur le segment [AB]
donc x [0;8]
1b) hauteur d'un triangle équilatéral = côté*3/2
CH = 8*3/2 = 43
1c) Thalès
en remarquant que MNAB , QPAB et CHAB
MN/CH = AM/AH
MN = CH*AM/AH
avec CH = 43
AM = x et AH=4 puisque la hauteur CH est aussi la médiane
MN = 43*x/4
MN = 3*x
1d) aire du rectangle MNPQ = MN*MQ
if faut donc calculer MQ
MQ = 2*MH (H est le milieu de MQ par symétrie)
MQ = 2*(4-x) = 8 - 2x
a(x) = 3*x*(8-2x)
développe puis met sous la forme canonique
Annuler
connectez vous