Inscription / Connexion Nouveau Sujet
analyse , polynome de degré 3
Bonsoir , j'ai un bon exercice d'analyse qui mérite réflexion ! :
Soient a,b,c,d des nombres réels avec a différent de 0 . On considère la fonction polynome , x appartient à R : f(x) ax³+bx²+cx+d .
1) Etudier les limites de f , quand f tend vers + l'infini et quand f tend vers - l'infini . En déduire que la fonction f s'annule au moins une fois sur R .
Ma réponse : quand x tend vers l'infini , si a>0 f tend vers l'infini , si a<0 f tend vers - l'infini . Quand x tend vers - l'infini c'est l'inverse vu que la fonction est impaire .
Comme la fonction est continue et qu'il existe un nombre a tel que f(a) < 0 et un nombre b tel que f(b) > 0 , alors il existe un nombre c tel que f(c) = 0 , donc f s'annule au moins une fois . ( th des valeurs intermédiaires ) .
2)Calculer la dérivée de f . Que représente la quantité b² - 3ac ?
f' = 3ax² + 2bx + x
alors pour retrouver b²-3ac je voulais faire comme pour les second degrés et factoriser par a :
a(3x² + 2bx/a + c/a) mais après c'est la misère je vois pas par quelle technique factoriser , quelqu'un connait la bonne technique ?
merci de votre aide .
Bonsoir.
f '(x) = 3ax² + 2bx + c.
Le discriminant de f '(x) est :  = 4b² - 12ac = 4(b² - 3ac).
= 4b² - 12ac = 4(b² - 3ac).
C'est son signe qui te dira si l'équation f ' (x) = 0 admet des solutions réelles ou non.
Il me semble que la conclusion
Quand x tend vers - l'infini c'est l'inverse vu que la fonction est impaire .
est un peu erronée car la fonction f n'est pas impaire (ni paire)
f(-x) = a(-x)3 + b(-x)2 + c(-x) + d = -ax3 + b(-x)2 - cx + d qui en général n'est
ni ax3 + bx2 + cx + d
ni -ax3 - bx2 - cx - d
erreurs de balises ... 
Il me semble que la conclusion
Quand x tend vers - l'infini c'est l'inverse vu que la fonction est impaire .
est un peu erronée car la fonction f n'est pas impaire (ni paire)
f(-x) = a(-x)3 + b(-x)2 + c(-x) + d = -ax3 + b(-x)2 - cx + d qui en général n'est égal
ni ax3 + bx2 + cx + d
ni -ax3 - bx2 - cx - d
Bonjour.
Je ne comprends pas ce qui te gène. Je redétaille :
f '(x) = 3ax² + 2bx + c.
du type : Ax² + Bx + C, avec A = 3a, B = 2b, C = c
 = B² - 4.A.C = (2b)² - 4.(3a).c = 4b² - 12ac = 4(b² - 3ac)
= B² - 4.A.C = (2b)² - 4.(3a).c = 4b² - 12ac = 4(b² - 3ac)
excuse moi raymond j'étais partie dans un délire pas possible à essayer de trouver le discriminant par factorisation de a comme pour le second degré si tu vois ce que je veux dire lol , je continue l'exercice il est bientot fini 
alors raymond oui j'ai plus que des questions sur ce discriminant , donc si le discriminant est égal à 0 je dois montrer que f s'annule une fois sur R , voici ma réponse :
si le discriminant est égal à 0 , la racine de la dérivée est -b/3a , donc la dérivée s'annule pour au point -b/3a , donc f est croissante et décroissante de l'un ou l'autre coté ( je saurai pas dire lequel ) , donc f forcément s'annule sur R .
que pensais vous de la justification ? ça me fait penser un peu à Rolle 
Dans la question 2°), on te demande simplement ce que représente b² - 3ac.
Tu réponds que c'est le discriminant réduit de l'équation f '(x) = 0.
Pour répondre à d'autres questions, il faut que tu nous les écrives.
oui la question c'est :
1) on suppose que discriminant = 0 . Montrer que f s'annule exactement une fois sur R .
si le discriminant est égal à 0 , la racine de la dérivée est -b/3a , donc la dérivée s'annule pour au point -b/3a , donc f est croissante et décroissante de l'un ou l'autre coté ( je saurai pas dire lequel ) , donc f forcément s'annule sur R du fait de sa continuité , mais c'est mal rédigé je crois.
2) on suppose que discriminant négatif , montrer que f s'annule une fois sur R avec tableau de variation et par l'absurde .
Alors là je dois avouer que je comprends pas car comment tracer le tableau de variations , si le discriminant est négatif il peut pas yavoir de racine réelle , on aurait :
-2b - bV(-3ac)/6a et -2b + bV(-3ac)/6a , ça ne rime à rien...
Si le discriminant est nul, cela signifie que le polynôme f '(x) a une racine unique x0.
Alors, f '(x) = 3a(x - x0)².
Donc, f ' s'annule une fois en x0, mais sans changer de signe : elle garde le signe de a.
Si a > 0 f est croissante, Si a < 0 f est décroissante.
Facile : f '(x) ne s'annule jamais, donc, garde toujours le signe de a.
En fait, tu es en train d'utiliser ce que l'on appelle en première : "le signe du trinôme".
Je t'en rappelle le principe.
Soit P(x) = ax² + bx + c un trinôme du second degré (donc a  0).
0).
Son dicriminant est  = b² - 4ac.
= b² - 4ac.
¤ Si  < 0.
< 0.
alors, pour tout x, P(x) est du signe de a.
¤ Si  = 0.
= 0.
alors, P(x) = a(x - x0)² où x0 = -(b/a) désigne l'unique racine. Donc, P(x) s'ammule en x0, mais garde le signe de a puisqu'un carré est toujours positif.
¤ Si  > 0.
> 0.
alors, P(x) a deux racines distinctes : x' et x". Dans ce cas, P(x) est du signe de a à l'extérieur des racines et du signe contraire de a entre les racines. En clair, en supposant x' < x" :
x < x' ou x > x" => P(x) du signe de a
x' < x < x" => P(x) du signe contraire de a.
oui ça je le connais par coeur mais ici c'est un polynime de degré 3 , toi tu parles de degré 2 qui est la dérivée mais la question concerne f et non f'... , et la question c'est :
si discriminant < 0 montrer que f s'annule 1 fois sur R en étudiant le tableau de variations de f .
ben finalement j'ai une réponse à te proposer raymond : comme le discriminant est négatif , la dérivée sera du signe de a , donc soit croissante soit décroissante , donc logiquement f s'annulera juste une fois sur R , qu'en penses tu ?
Je ne me suis pas trompé en parlant du second degré : il s'agit bien d'étudier le signe de la dérivée f ' pour connaître les variations de f.
Ta conclusion est la bonne.
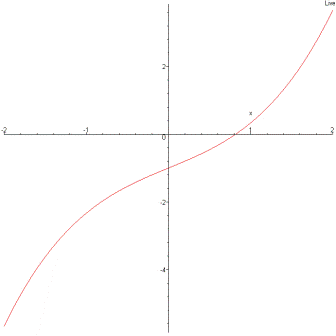
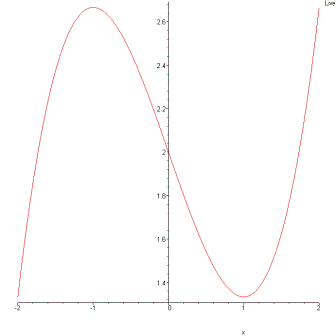
Je t'adresse trois dessins de la fonction f, (en supposant a > 0) suivant le signe de la dérivée.
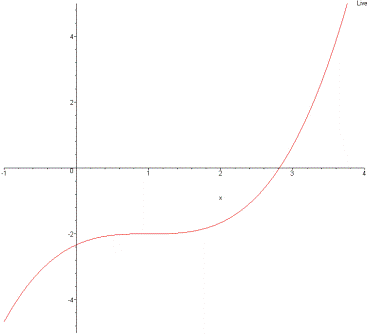
merci bien raymond , j'aurais aimé savoir prouvé ça par l'absurde mais j'ai pas réussi , encore merci bcp de ton aide et tes explications très détaillés .
raymond une petite question très importante : est ce que pour le discriminant positif ya un rapport avec le théorème de rolle ?
merci
Non, le théoréme de Rolle impose à f de s'annuler en deux points a et b. Dans ce cas, tu peux affirmer qu'il existe c tel que a < c < b et f '(c) = 0.
Le dernier dessin que je t'ai envoyé montre une fonction du troisième degré dont la dérivée a un discriminant strictement positif, donc, la dérivée possède deux racines distinctes (ici, -1 et 1). Pourtant, cette fonction ne s'annule qu'une seule fois (vers -2).


 algèbre en Bts
algèbre en Bts