Inscription / Connexion Nouveau Sujet
Applications linéaires
Bonjour, j'ai la figure ci-joint, dans R2.
On la projection de P(
).
Si on est dans la base B=(
Je n'arrive pas à voir comment déduire l'expression analytique de P ...
Désolé je n'ai pas vraiment de "texte" pour le sujet de l'exercice.
Les vecteurs sont pour la question suivante
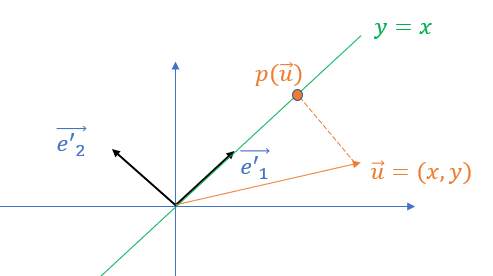
La distance entre |p(u)| entre O et p(u) est l'un des côtés d'un triangle rectangle d'hypoténuse |u|.
Si tu appelles \theta l'angle entre et
et
celui entre
et
(c'est à dire
),
tu as
et bien-sûr, .
La difficulté est le choix de l'intervalle pour . Si tu es dans
c'est simplement
, mais attention aux cas où u est horizontal ou vertical
Bonsoir et merci pour votre réponse.
J'ai du mal à comprendre ce qu'on obtient avec votre réponse, sachant que la question suivant est : Déterminer A = MB(P).
En fait, cela ressemble très peu aux exercices que j'ai fais précédemment sur les applications linéaires. Je n'arrive pas à trouver comment exprimer P dans la base. La méthode que vous avez envoyé, je ne vois pas comment on peut retrouver une expression analytique, utilisable pour la question suivante par exemple.
salut
avec u(x,y)
posons P(x,y)=(xo,yo) la projection orthogonale du vecteur v(x,y) sur la droite D d'équation y=x , comme (xo,yo) appartient à D alors xo=yo.
on aussi u - P(u) appartient à la droite y=-x soit (xo- x , yo -y) appartient à y=-x
on a donc yo- y = -xo+x soit
ensuite c'est tout simple il suffit d'obtenir P(x,y) = (xo,yo) grace à
yo- y = -xo+x
xo=yo.
a toi d'exprimer xo en fonction de x et y et aussi yo en fonction de x et y et tu obtiendra
l'expression de P(x,y) en fonction de x et y


 algèbre en Bts
algèbre en Bts