Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques
Niveau Maths sup
Partager :

Arc paramétré

Posté par
mj4 26-10-11 à 11:56

Bonjour, j'ai un exercice à faire, j'en ai réussi une partie pourriez vous vérifier si c'est juste, pour que je puisse réfléchir sur la suite?

Voici l'énoncé:

x(t)=cos3(t)
y(t)= sin(t) * (2cos2(t) +1)/2

Voici ma réponse:

donc x et y sont 6 périodique
x(t+3)=-x(t)
y(t+3)=y(t)
donc une symétrie par rapport à l'axe Oy

x((-t)=x(t)
y(-t)=-y(t)
donc une symétrie par rapport à l'axe Ox

donc De=[;+3]
on centre en 0 et on obtient De=[0;3/2] suivi de SOy suivi de SOx
(c'est bien dans cet ordre?)

pas d'étude aux bornes

donc ensuite j'ai fait mon tableau de variation (sur word) que j'ai inséré


Voila je me suis arrêtée ici , pour voir si tout ca était déjà juste, car j'ai beaucoup de mal à tracer les courbes


Merci d'avance

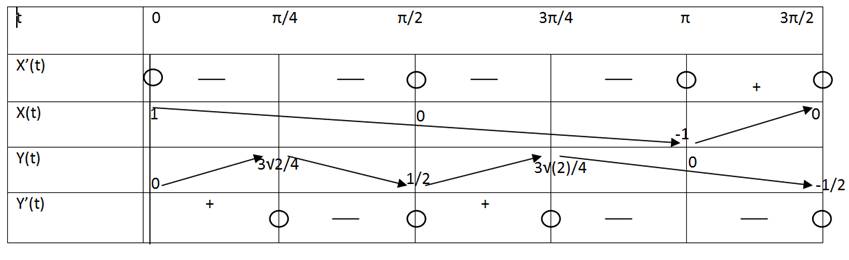
Arc paramétré

Posté par
dhaltere : Arc paramétré 26-10-11 à 12:32

déjà, x et y sont 2\pi périodiques

ensuite
x(-t)=-x(t)
y(-t)=-y(t), ce qui indique une symétrie par rapport à l'origine du repère

ensuite
x(\pi-t)=-x(t) \\ y(\pi-t)=y(t)
ce qui indique une symétrie par rapport à l'axe des ordonnées

donc ces deux symétries impliquent aussi la symétrie par rapport à l'axe des abscisses

on étudie la courbe pour la branche x\ge0, y\ge0
c'est à dire qu'on peut se limiter à 0\le t\le \frac{\pi}2

Posté par
mj4re : Arc paramétré 26-10-11 à 19:18

d'accord, je vais chercher mes erreurs
et je vais recommencer le tableau

Posté par
dhaltere : Arc paramétré 26-10-11 à 20:39

sur [0;\frac{\pi}2]
Arc paramétré

sur une période [0;2\pi]
Arc paramétré

Posté par
mj4re : Arc paramétré 26-10-11 à 21:34

D'accord, merci beaucoup, je vais essayer de refaire vos courbe, par contre, en faite j'ai plusieurs question:
-quand on a des cosinus et des sinus dans des equations paramétrique la période est toujours de 2?

- et aussi je pense que cela revient au même mais dans mon cours on me dit de calculer : x(t+ période/2) et y(t+période/2)
x(t+)=-x(t)
y(t+)=-y(t)
et
x(-t)=x(t)
y(-t)=-y(t)

donc De=[0;] suivi d'une symétrie par rapport à l'axe Ox, suivi d'une symétrie par rapport à l'origine du repère O

et j'obtiens le tableau de variations que j'ai inséré

Merci d'avance

Arc paramétré

Posté par
dhaltere : Arc paramétré 26-10-11 à 23:47

ton tableau est à peu près correct, le maximum est atteint en t=\frac{\pi}4
mais ton calcul du maximum est erroné : A=(\frac{\sqrt2}4 ; \frac{\sqrt2}2)

il y a une tangente verticale en t=0, point (1;0)
par contre, lorsque t tend vers \frac{\pi}2, les deux dérivées tendent vers 0, et la pente est indéterminée.

L'étude du rapport montre que la tangente tend vers la verticale au voisinage de t=\frac{\pi}2, au point de coordonnées (0;1/2), mais son module, c'est à dire la vitesse du point mobile, tend vers 0.


-quand on a des cosinus et des sinus dans des équations paramétriques la période est toujours de 2\pi?

x=cos(1/2t)
y=sin(3/5t)

Arc paramétré

périodicité 20\pi

x=t+cos(1/2t)
y=sin(1/2t)

Arc paramétré

périodicité de 4\pi, mais seulement le long de l'axe des abscisses

x=\cos(t) \\ y=\sin(\sqrt 2t)

Arc paramétré

en fait j'ai limité l'affichage, mais la courbe remplit le carré;
elle n'a aucune périodicité.

Posté par
mj4re : Arc paramétré 27-10-11 à 18:52

D'accord, merci beaucoup, par contre je 'nai pas comrpis comment vous trouviez la pente de la tangente au point d'abscisse /2 parce que  en faisant y'(t)/x'(t) on a une valeur indeterminée, comme vous l'avez dit, et on obtient la même chose avec
(y(t)-b)/(x(t)-a) = ( y(t)-0,5)/x(t)

et cela revient bien au même le tracé de la courbe avec les symétrie que j'ai obtenue : De=[0;] suivi d'une symétrie par rapport à l'axe Ox, suivi d'une symétrie par rapport à l'origine du repère O

Merci d'avance

Posté par
dhaltere : Arc paramétré 27-10-11 à 19:17

Citation :
et cela revient bien au même le tracé de la courbe
J'en suis fort aise.

une forme indéterminée, ça se travaille en espérant lever l'indétermination.

tu vas trouver, si tu cherches un peu, que le rapport est égal à -\text{cotan}(2t) (de mémoire)

la limite quand t\rightarrow\frac{\pi}2,\quad t<\frac{\pi}2 est  -\infty

Je voudrais bien savoir si tu as trouvé seule que y'(t) s'annulait en \frac{\pi}4, vu les erreurs qui suivaient, calcul de y(\frac{\pi}4) et la difficulté que tu rencontres à modifier \frac{y'}{x'} pour lever l'indétermination.

Posté par
mj4re : Arc paramétré 27-10-11 à 21:11

d'accord, merci beaucoup, je vais y réfléchir,
pour trouver que y'(t) s'annulait en /4, j'avoue que je me suis aidée de ma calculatrice, mais il faudra que je cherche à modifier l'expression pour le trouver sans calculatrice,
et quand je disais que  "cela revient bien au même le tracé de la courbe" j'ai oublié un point d'interrogation, car je n'était pas sûre de moi,

et dans la suite de mon exercice on me demandede vérifier que:
-le cercle unité est tangent à la courbe
-les droites d'équations (x=2/2) et (y=-2/2) sont tangentes en deux points à la courbe
-les droites d'équations (y=-(x+1)/3) et (y=(x-1)/3) sont tangenets en un point de la courbe
pourriez vous me donner quelques pistes ou indices?

Merci d'avance

Posté par
dhaltere : Arc paramétré 27-10-11 à 22:21

je me disais aussi

y(t)=\sin(t)\frac{2\cos(t)^2+1}2

y'(t)=\cos(t)\frac{2\cos(t)^2+1}2+\sin(t)\frac{-4\sin(t)\cos(t)}2

y'(t)=\frac{\cos(t)}2(2\cos(t)^2+1-4\sin(t)^2)

et on utilise les relations
\cos(2t)=2\cos(t)^2-1=1-2\sin(t)^2

y'(t)=\frac{\cos(t)}2([2\cos(t)^2-1]+1+1+2([1-2\sin(t)^2]-1))

y'(t)=\frac{\cos(t)}2(\cos(2t)+2\cos(2t))

y'(t)=\frac32\cos(t)\cos(2t)

s'annule sur [0;\frac{\pi}2] pour x=\frac{\pi}2 et x=\frac{\pi}4

Citation :
-le cercle unité est tangent à la courbe


au point (1;0) qui appartient à ce cercle unité, x'(0)=0, y'(0)=\frac32 : tangente verticale, tout comme celle de ce point sur ce cercle.

Citation :
-les droites d'équations (x=2/2) et (y=-2/2) sont tangentes en deux points à la courbe

faux pour (x=2/2), mais tu voulais sûrement dire (y=2/2)

Pour (y=2/2)
On a vue que le point de coordonnées (2\sqrt2/2, \sqrt2/2) est le sommet de la courbe dans le cadran principal, il admet une tangente horizontale, qui est cette droite
par symétrie % axe Oy, la droite est conservée, le point (-2\sqrt2/2, \sqrt2/2) est l'autre point de tangence

Pour (y=-2/2)
par symétrie par rapport à Ox, on obtient ces deux points de tangence avec cette droite

Citation :
-les droites d'équations (y=-(x+1)/3) et (y=(x-1)/3) sont tangentes en un point de la courbe


oui, et aussi y=(-x+1)/3 et y=(x+1)/3
ces quatre droites sont obtenues de par les symétries Ox et Oy

traitons le cas y=(x+1)/3
cette droite semble tangente dans le premier cadran

Le plus simple est de chercher les points de la courbe dont la tangente a un coefficient directeur de \frac1{\sqrt3}

il faut résoudre
\frac{y'}{x'}=-\frac1{\tan(2t)}=\frac1{\sqrt3} dans [0,\frac{\pi}2]

or \tan(\alpha)=-\sqrt3 sur [0;\pi] a pour unique solution \frac23\pi

donc le point de la courbe à l'abscisse curviligne t=\frac{\pi}3 admet une tangente de pente \frac1{\sqrt3}

reste à vérifier que ce point est sur la droite

le calcul de ses coordonnées donne (\frac18;\frac{3\sqrt3}8)

en substituant dans l'équation de la droite, on obtient
\sqrt3\frac{3\sqrt3}8=\frac98
équation vérifiée.

Arc paramétré

Posté par
mj4re : Arc paramétré 27-10-11 à 22:38

d'accord,merci beaucoup de vous donner autant de mal, je suis en train de regarder, j'ai aussi réussi à retrouver y'(t) simplifié, (sans regarder ce que vous avez fait), sauf que moi il m'a fallu une page

et je vais essayer de lever l'indétermination en /2
pour la pente de la tangente

Posté par
dhaltere : Arc paramétré 27-10-11 à 22:42

oh, si je n'en tirais pas de temps en temps une certaine satisfaction, je ne le ferais pas.

Posté par
mj4re : Arc paramétré 28-10-11 à 19:28

D'accord, en faite je ne comprend pas comment vous trouver les coordonnées du point (1;0) et que vous pouvez dire qu'il est tangent au cercle

Merci d'avance

Posté par
dhaltere : Arc paramétré 28-10-11 à 19:52

t=0 --> x(0)=1 et y(0)=0, donc le point de coordonnées (1,0) fait partie de la courbe, époustouflant, non ?

de plus x'(0)=0 et y'(0)=3/2, donc la tangente a pour vecteur directeur un vecteur de coordonnées (0,3/2)
si c'est pas vertical, ça

Posté par
mj4re : Arc paramétré 28-10-11 à 21:20

d'accord, j'ai compris,
j'ai aussi compris votre méthode pour les droites d'équation(y=-(x+1)/3) et (y=(x-1)/3)
je suis en train de réfléchir pour les droites d'équations (y=2/2) et (y=-2/2)

Posté par
dhaltere : Arc paramétré 28-10-11 à 21:32

elles sont pourtant plus simples

Posté par
mj4re : Arc paramétré 29-10-11 à 19:43

oui en faite j'ai compris le principe mais ce que je ne comprend pas c'est les coordonées du point parce que dans le tableau on avait dit que son abscisse était 2/4 alors pourquoi là on met 22/4

et en faite pour les droites d'équation(y=-(x+1)/3) et
(y=(x-1)/3)
j'ai compris le principe mais je ne vois pas comment vous faite pour  obtenir 2/3 après avoir dit que tan()=-3
sur[0;]

Merci d'avance

Posté par
dhaltere : Arc paramétré 29-10-11 à 20:23

tu confonds abscisses et ordonnées

le maximum est A=(\frac{\sqrt2}4 ; \frac{\sqrt2}2)

y= \frac{\sqrt2}2 est la tangente horizontale qui passe par ce maximum.

pourquoi j'obtiens \frac{2\pi}3 comme solution de l'équation \tan(\alpha)=-\sqrt3 sur l'intervalle [0;\pi] ?

alors là, tu demandes vraiment des explications sur des choses que tu devrais largement maîtriser.

\sin(\frac{\pi}3)=\frac{\sqrt3}2 \\ \cos(\frac{\pi}3)=\frac12
J'espère que là, tu suis...

le rapport des deux donne
\tan(\frac{\pi}3)=\frac{\sin(\frac{\pi}3)}{\cos(\frac{\pi}3)}=\sqrt3

on utilise
\sin(\pi-\beta)=\sin(\beta) \\ \cos(\pi-\beta)=-\cos(\beta) \\ \tan(\pi-\beta)=-\tan(\beta)

\tan(\pi-\frac{\pi}3)=-\sqrt3

voilà pourquoi
\tan(\frac{2\pi}3)=-\sqrt3


plus pratique, au brouillon, tu traces un cercle trigonométrique, et tu reportes -\sqrt3 sur la droite verticale qui passe par (1;0)
puis tu traces l'oblique : elle te donne les angles solutions de l'équation

Arc paramétré

Posté par
mj4re : Arc paramétré 29-10-11 à 21:20

d'accord, merci beaucoup je n'avais pas pensé à modifier la relation avec la tangente de cette façon donc ,si j'ai juste pour la tangente d'équation y= (-x+1)/(3) en ayant fait votre petit schéma je trouve que 2t=4/3
donc t=2/3

et après pour l'autre équation je fais une symétrie par rapport à l'axe Ox

Posté par
dhaltere : Arc paramétré 29-10-11 à 21:48

oui, mais là encore, il y a beaucoup plus simple maintenant que le cas y=\frac{x+1}{\sqrt3} a été traité

la droite y=\frac{-x+1}{\sqrt3} s'obtient par symétrie par rapport à Oy

Or, c'est la transformation t\rightarrow \pi-t qui transforme x(t) en -x(t) et conserve y(t), c'est à dire qui effectue la symétrie par rapport à Oy de la branche de la courbe du premier cadran.

la droite y=\frac{x+1}{\sqrt3} est tangente à la courbe en t=\frac{\pi}3

donc la droite symétrique y=\frac{-x+1}{\sqrt3} sera tangente à la courbe en t=\pi-\frac{\pi}3=\frac{2\pi}3

Cette explication peut te paraître plus longue que ta propre démonstration, mais c'est surtout parce que je l'ai détaillée.
L'étude initiale des symétries nous a permis d'étudier la courbe sur un intervalle réduit, autant continuer à utiliser ces symétries pour répondre aux questions suivantes.

Dernière remarque : il est rassurant de voir que les deux méthodes mènent au même résultat.

Posté par
mj4re : Arc paramétré 29-10-11 à 22:04

d'accord, j'ai compris, merci beaucoup pour votre aide et vos explications , et bonne continuation

Posté par
mj4re : Arc paramétré 31-10-11 à 09:02

Bonjour dhalte, je voulais vous demander si vous vous y connaissiez en science de l'ingénieur, parce que j'ai quelques exercice et je bloque, je ne trouve personne pour m'aider

Merci d'avance

Posté par
dhaltere : Arc paramétré 31-10-11 à 11:02

pas spécialement en sciences de l'ingénieur

si tes exercices ont une coloration physique, je te conseille de les soumettre dans le forum correspondant : https://www.ilephysique.net/

sinon, tu peux les soumettre dans ce forum maths, tu verras bien si tu trouves quelqu'un pour t'aider.

Posté par
lulucyfer93petit complément. 31-10-11 à 11:23

je ne veux pas tout gacher mais il me semble que la courbe représentative de ta fonction paramétrée ressemble plutôt à ça ... :

petit complément.

Posté par
dhaltere : Arc paramétré 31-10-11 à 11:32

bravo lulucyfer93 pour ta pertinence

x(t)=\cos(t)^3 \\ y(t)= \sin(t) * \frac{2\cos(t)^2 +1}2

Nous remarquerons évidemment que la suite de l'énoncé qui demande à établir les tangences des droites y=\frac{\sqrt2}2,\quad y=-\frac{x+1}{\sqrt3} avec la courbe est alors complètement erronée.

Pas grave, lulu va nous expliquer comment elle a tracé cette courbe qui contredit manifestement tout ce qui a été établi auparavant, énoncé comme résultats.

Posté par
mj4re : Arc paramétré 31-10-11 à 17:59

je ne comprends pas parce que j'ai vérifié sur maple et j'obtiens la première courbe

Posté par
dhaltere : Arc paramétré 31-10-11 à 18:56

quelle première courbe ? et les signes, les parenthèses, et autres erreurs stupides, Maple ne saura pas te les indiquer.

je t'assure que les courbes obtenues sont celles que j'ai indiquées

je suis sûr que Maple, bien utilisé, ne me contredira pas.

Posté par
mj4re : Arc paramétré 31-10-11 à 19:36

Oui, je parlais de votre courbe, maple me donne votre courbe

Posté par
dhaltere : Arc paramétré 31-10-11 à 19:48

on va attendre que lulucyfer93 donne plus d'explications.

Posté par
lulucyfer93re : Arc paramétré 31-10-11 à 22:05

excusez moi il me semble que mon logiciel de traçage de courbe ait fait une petite erreur. Je ne  comprends toujours pas pourquoi j'obtiens ceci alors que j'ai demandé l'arc paramétré en question. Je reposte qqch si ça s'arrange. Désolé pour le dérangement.

Posté par
dhaltere : Arc paramétré 31-10-11 à 22:15

Citation :
il me semble que mon logiciel de traçage de courbe ait fait une petite erreur.


non, il a fait ce que tu lui demandais de faire
si il y a eu une erreur, ce n'est pas de son fait.

accuser quelqu'un qui ne peut pas se défendre, c'est pas bien.

Posté par
lulucyfer93re : Arc paramétré 31-10-11 à 22:17

ma calculette et mon ordi ne semblent pas être d'accord sur les courbes que je leur demande :/ mais pour ce petit bug passager (de ma part certainement), veuillez m excuser.

Posté par
dhaltere : Arc paramétré 31-10-11 à 22:20

faute avouée est à moitié pardonnée

pour pénitence, tu relieras 3 fois le manuel d'utilisation

Posté par
lulucyfer93re : Arc paramétré 31-10-11 à 22:20

effectivement en redémarrant mon ordi le bug a disparu

Posté par
lulucyfer93re : Arc paramétré 31-10-11 à 22:21

ouais enfin je le lirai un autre jour promis j ai d'autres choses à faire présentemment, bonne soirée ^^ !

Posté par
dhaltere : Arc paramétré 31-10-11 à 22:26

ha, les promesses n'engagent que ceux qui les écoutent...

ne remets jamais au lendemain ce que tu peux faire le surlendemain,

et autres aphorismes inspirés...

allez, l'ordinateur écope pour punition de t'offrir de jolis fonds d'écran colorés.


Rechercher
Menu
Espace membre
24 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1734 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !